Để biểu thức N có nghĩa thì:
\(\sqrt{x-6}>0\)=> x - 6 > 0 => x > 6
\(Để\) N có nghĩa thì : \(\left\{{}\begin{matrix}\sqrt{x-6}\ge0\\\sqrt{x-6}\ne0\end{matrix}\right.=>\sqrt{x-6}>0=>x-6>0=>x>6\)
Vậy để N có nghĩa thì x > 6
\(b.\sqrt{x^2-6x+9}=5\)
\(\Leftrightarrow\)\(\sqrt{\left(x-3\right)^2}=5\)
\(\Leftrightarrow\)\(\left|x-3\right|=5\)\(\Rightarrow\)Với x \(\ge3\)\(\Rightarrow\) \(x=8\)
Với x \(< 3=>x=-2\)






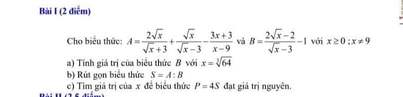

 giúp mk với
giúp mk với