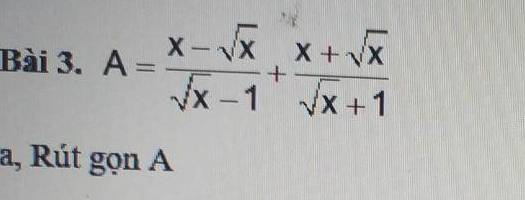Câu 1: A
Câu 2: D
Câu 3: B
Câu 4: C
Bài 1:
a)
\(A=\left(\frac{4\sqrt{x}}{\sqrt{x}+2}-\frac{8x}{(\sqrt{x}-2)(\sqrt{x}+2)}\right):\left(\frac{\sqrt{x}-1}{\sqrt{x}(\sqrt{x}-2)}-\frac{2(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}\right)\)
\(=\frac{4\sqrt{x}(\sqrt{x}-2)-8x}{(\sqrt{x}-2)(\sqrt{x}+2)}:\frac{\sqrt{x}-1-2(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}=\frac{-4x-8\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}(\sqrt{x}-2)}{-\sqrt{x}+3}\)
\(=\frac{-4\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}(\sqrt{x}-2)}{3-\sqrt{x}}=\frac{-4x(\sqrt{x}-2)}{(\sqrt{x}-2)(3-\sqrt{x})}=\frac{4x}{\sqrt{x}-3}\)
b)
Ta có:
\(m(\sqrt{x}-3).A>x+2025\)
\(\Leftrightarrow 4xm>x+2025\Leftrightarrow x(4m-1)>2025\)
\(\Leftrightarrow 4m-1>\frac{2025}{x}\Leftrightarrow m>\frac{1}{4}(\frac{2025}{x}+1)\) với mọi $x>9$
\(\Leftrightarrow m> \max \frac{1}{4}(\frac{2025}{x}+1), \forall x>9\Leftrightarrow m>56,5\)
Bài 2:
a)
\(\left\{\begin{matrix} 4x-3y=19\\ 2x+3y=11\end{matrix}\right.\Rightarrow 6x=30\Rightarrow x=5\)
\(y=\frac{4x-19}{3}=\frac{4.5-19}{3}=\frac{1}{3}\)
b)
\(3x^2-20x+12=0\Leftrightarrow (x-6)(3x-2)=0\)
\(\Rightarrow \left[\begin{matrix} x=6\\ x=\frac{2}{3}\end{matrix}\right.\)
Bài 3:
Giả sử vòi 1 và vòi 2 chảy một mình trong lần lượt $a$ và $b$ giờ thì đầy bể.
Khi đó, trong 1 giờ:
Vòi 1 chảy được $\frac{1}{a}$ bể
Vòi 2 chảy được $\frac{1}{b}$ bể
Theo bài ra ta có: \(\left\{\begin{matrix} \frac{1}{a}+\frac{1}{b}=\frac{9}{40}\\ \frac{3,6}{a}+\frac{3,6+0,4}{b}=\frac{85}{100}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{1}{a}+\frac{1}{b}=\frac{9}{40}\\ \frac{3,6}{a}+\frac{4}{b}=\frac{17}{20}\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \frac{1}{a}=\frac{1}{8}\\ \frac{1}{b}=\frac{1}{10}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=8\\ b=10\end{matrix}\right.\)
Vậy vòi 1 chảy trong 8 giờ sẽ đầy bể.
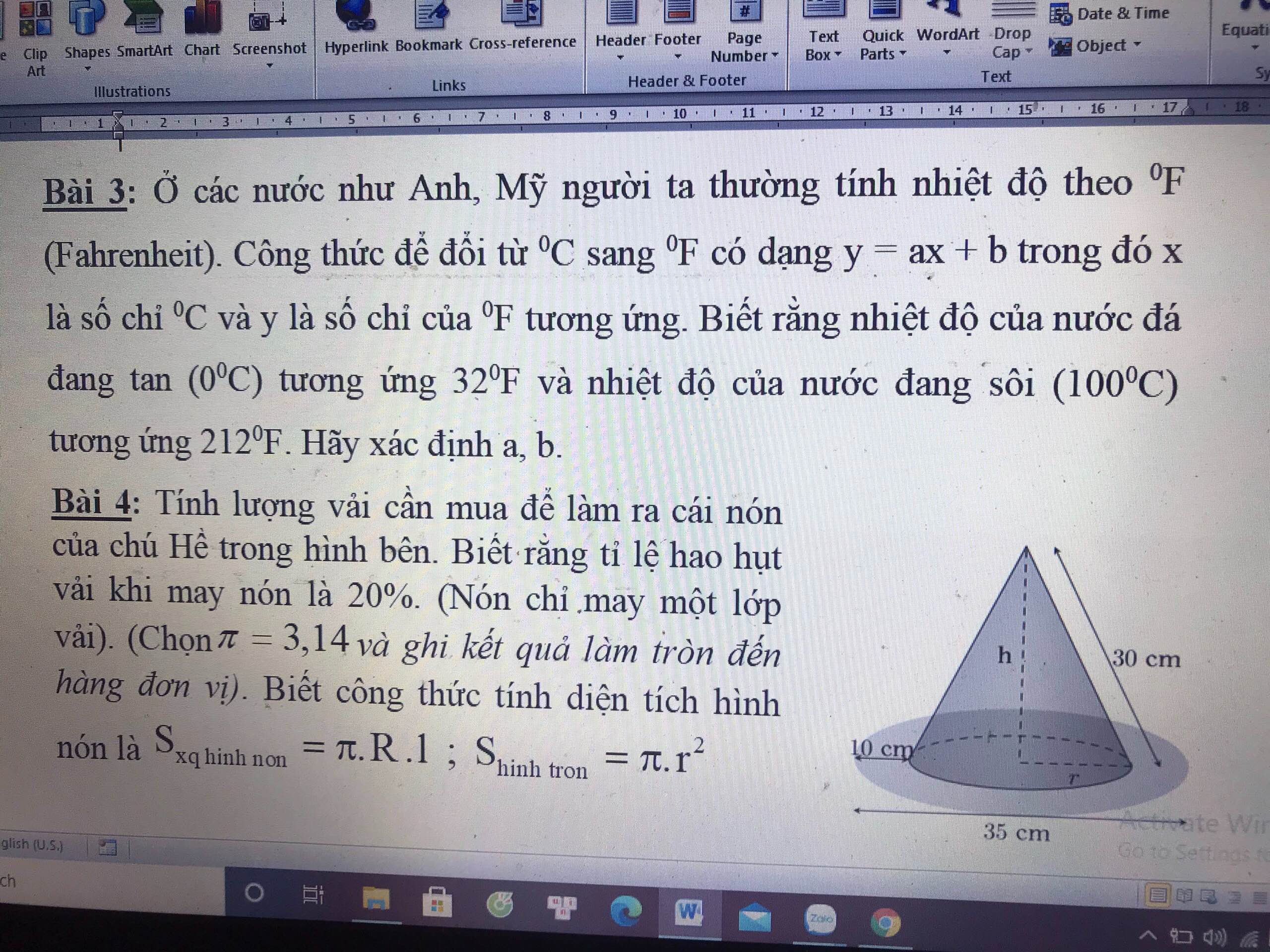
Bài 4:
Để pt có nghiệm $x_1,x_2$ thì:
$\Delta'=m^2-m+1\geq 0\Leftrightarrow (m-\frac{1}{2})^2+\frac{3}{4}\geq 0$
$\Leftrightarrow m\in\mathbb{R}$
Khi đó, áp dụng định lý Viet:
\(\left\{\begin{matrix} x_1+x_2=2m\\ x_1x_2=m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=8\Leftrightarrow (x_1+x_2)^2-2x_1x_2=8\)
\(\Leftrightarrow (2m)^2-2(m-1)=8\Leftrightarrow 2m^2-m+1=4\)
\(\Leftrightarrow 2m^2-m-3=0\Leftrightarrow (m+1)(2m-3)=0\Rightarrow m=-1\) hoặc $m=\frac{3}{2}$
Bài 6:
\(4x^2+xy+4y^2=\frac{1}{2}(x+y)^2+\frac{7}{2}(x^2+y^2)\)
Áp dụng BĐT Cô-si:
$x^2+y^2\geq 2xy\Rightarrow 2(x^2+y^2)\geq (x+y)^2$
$\Rightarrow x^2+y^2\geq \frac{(x+y)^2}{2}$
$\Rightarrow \frac{7}{2}(x^2+y^2)\geq \frac{7}{4}(x+y)^2$
$\Rightarrow 4x^2+xy+4y^2\geq \frac{9}{4}(x+y)^2$
$\Rightarrow \sqrt{4x^2+xy+4y^2}\geq \frac{3}{2}(x+y)$
Tương tự suy ra:
$B\geq 3(x+y+z)$
Áp dụng BĐT Bunhiacopxky:
$3(x+y+z)=(1+1+1)(x+y+z)\geq (\sqrt{x}+\sqrt{y}+\sqrt{z})^2=1$
$\Rightarrow B\geq 1$
Vậy $B_{\min}=1$. Giá trị này đạt tại $x=y=z=\frac{1}{9}$
Bài 5:
a)
$HM\perp AB, HN\perp AC$ nên $\widehat{AMH}=\widehat{ANH}=90^0$
Tứ giác $AMHN$ có tổng 2 góc đối nhau $\widehat{AMH}+\wideat{ANH}=90^0+90^0=180^0$ nên là tứ giác nội tiếp.
b)
Vì $AMHN$ nội tiếp nên $\widehat{AMN}=\widehat{AHN}$
Mà $\widehat{AHN}=\widehat{ACB}$ (cùng phụ $\widehat{NHC}$)
$\Rightarrow \widehat{AMN}=\widehat{ACB}$
Xét tam giác $AMN$ và $ACB$ có:
$\widehat{A}$ chung
$\widehat{AMN}=\widehat{ACB}$ (cmt)
$\Rightarrow \triangle AMN\sim \triangle ACB$ (g.g)
c)
Vì $AQBC$ là tứ giác nội tiếp nên:
$PQ.PA=PB.PC(1)$
Vì $\widehat{AMN}=\widehat{ACB}$ nên $BMHC$ là tứ giác nội tiếp
$\Rightarrow PM.PN=PB.PC(2)$
Từ $(1);(2)\Rightarrow PQ.PA=PM.PN$
$\Rightarrow AQMN$ là tứ giác nội tiếp
Hay $A,Q,M,N$ cùng thuộc đtron
Ở phần a, ta cũng chỉ ra $A,M,H,N$ cùng thuộc đtron
Do đó: $A,Q,M,N,H$ cùng thuộc đường tròn
$\Rightarrow AQMH$ là tứ giác nội tiếp
$\Rightarrow \widehat{AQK}=\widehat{AQH}=\widehat{AMH}=90^0$
$\Rightarrow AK$ là đường kính của $(O)$
$\Rightarrow \widehat{ACK}=90^0$ (góc nt chắn nửa đường tròn)
Ta có đpcm.