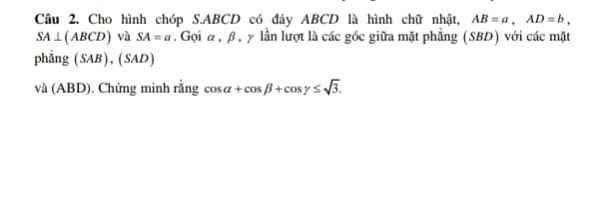1.
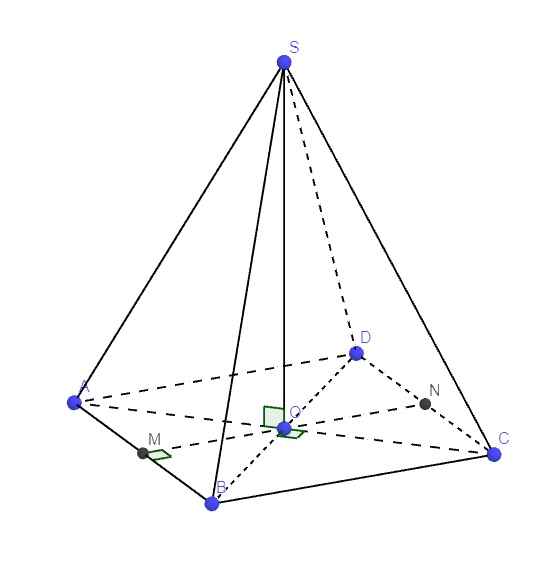
Gọi O là giao điểm AC và BD
Do chóp S.ABCD là chóp đều \(\Rightarrow\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\\AC\perp BD\end{matrix}\right.\)
a.
Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp BD\\AC\perp BD\end{matrix}\right.\)
\(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(BD\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)
b.
M; N lần lượt là trung điểm AB, CD \(\Rightarrow MN\) là đường trung bình của hình vuông ABCD
\(\Rightarrow MN\perp AB\) và \(O\in MN\) \(\Rightarrow SO\in\left(SMN\right)\)
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp AB\\AB\perp MN\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SMN\right)\)
Mà \(AB\in\left(SAB\right)\Rightarrow\left(SMN\right)\perp\left(SAB\right)\)
\(\left\{{}\begin{matrix}CD||AB\\AB\perp\left(SMN\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SMN\right)\)
Mà \(CD\in\left(SCD\right)\Rightarrow\left(SMN\right)\perp\left(SCD\right)\)
2.
a.
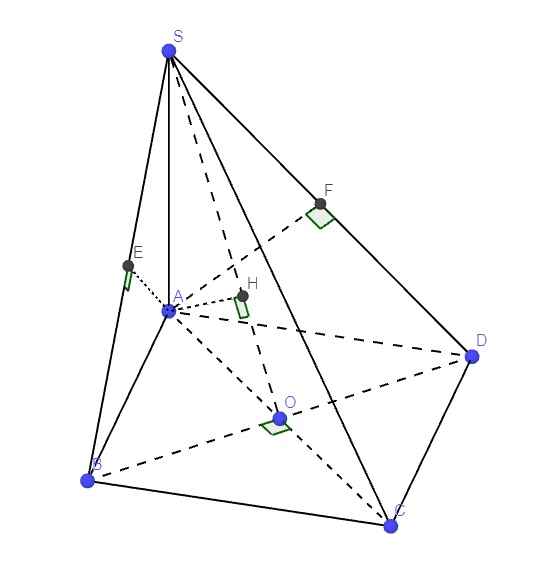
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(BD\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(BC\in\left(SBC\right)\Rightarrow\left(SBC\right)\perp\left(SAB\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(CD\in\left(SCD\right)\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
b.
Theo cmt, ta có: \(BC\perp\left(SAB\right)\Rightarrow BC\perp AE\)
Mà \(AE\perp SB\left(gt\right)\)
\(\Rightarrow AE\perp\left(SBC\right)\)
Hoàn toàn tương tự: \(\left\{{}\begin{matrix}CD\perp\left(SAD\right)\Rightarrow CD\perp AF\\AF\perp SD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AF\perp\left(SCD\right)\)
\(\left\{{}\begin{matrix}BD\perp\left(SAC\right)\Rightarrow BD\perp AH\\AH\perp SO\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBD\right)\)
3.
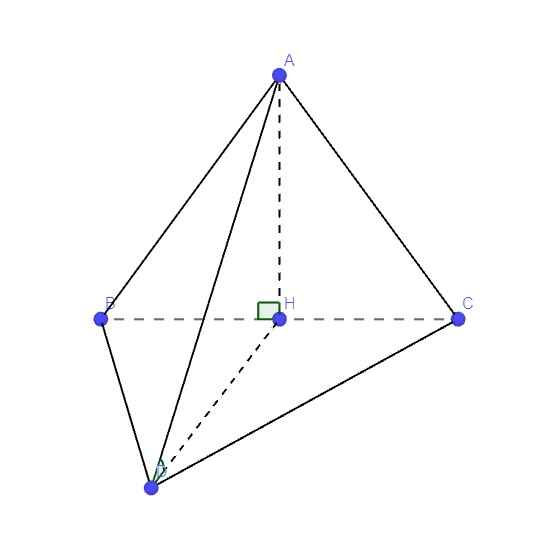
Gọi H là trung điểm BC
\(\Rightarrow AH\perp BC\) (tam giác ABC đều nên AH là trung tuyến đồng thời là đường cao)
Mà \(\left\{{}\begin{matrix}BC=\left(ABC\right)\cap\left(BCD\right)\\\left(ABC\right)\perp\left(BCD\right)\end{matrix}\right.\)
\(\Rightarrow AH\perp\left(BCD\right)\)
\(\Rightarrow AH\) là đường cao của chóp hạ từ A
\(AH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
b.
Do \(AH\perp\left(BCD\right)\Rightarrow\) DH là hình chiếu vuông góc của AD lên (BCD)
\(\Rightarrow\widehat{ADH}\) là góc giữa AD và (BCD)
\(\Rightarrow\widehat{ADH}=\varphi\)
\(\Rightarrow AD=\dfrac{AH}{sin\widehat{ADH}}=\dfrac{a\sqrt{3}}{2sin\varphi}\)
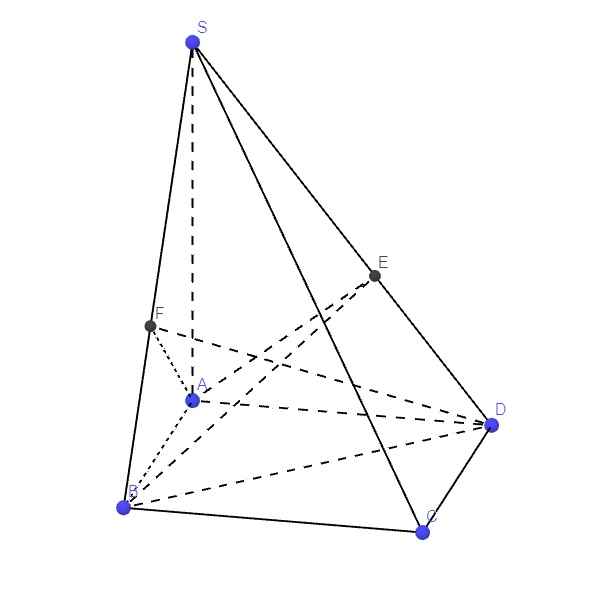
Bài 5:
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\Rightarrow AD\perp SB\)
Mà \(DF\perp SB\) (gt)
\(\Rightarrow SB\perp\left(ADF\right)\Rightarrow SB\perp AF\) (1)
\(\left\{{}\begin{matrix}BC||AD\\AD\perp\left(SAB\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AF\) (2)
(1);(2) \(\Rightarrow AF\perp\left(SBC\right)\Rightarrow\left(ACF\right)\perp\left(SBC\right)\)
b.
Theo cmt, \(AF\perp\left(SBC\right)\Rightarrow AF\perp SC\) (3)
Hoàn toàn tương tự câu a, ta chứng minh được \(AE\perp\left(SCD\right)\)
\(\Rightarrow AE\perp SC\) (4)
(3);(4) \(\Rightarrow SC\perp\left(AEF\right)\)
\(\Rightarrow\left(AEF\right)\perp\left(SAC\right)\)