Chương I - Căn bậc hai. Căn bậc ba
Các câu hỏi tương tự
Cho \(x;y;z>0\)
Tìm giá trị nhỏ nhất:
\(A=\dfrac{x^2}{x+yz}+\dfrac{y^2}{y+zx}+\dfrac{z^2}{z+xy}+\dfrac{9}{8\left(x^2+y^2+z^2\right)}\)
17 tháng 8 2021 lúc 17:54
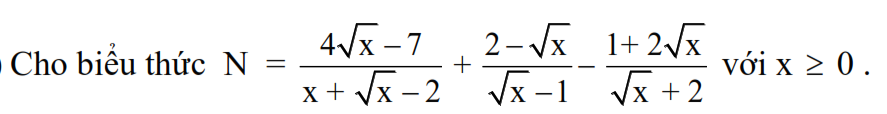
a) Tìm x để N=\(\dfrac{1}{2}\)
b) Tìm x ∈ \(Z\) sao cho N ∈ \(Z\)
c) Tìm GTLN của N
cho A= ( 1/căn x+1 - 2 căn x-2/ x căn x- căn x+x -1):( 1/căn x-1- 2/ x-1)
a) rút gọn A
b)tìm x thuộc Z để A thuộc Z
c)tìm x để A đạt GTNN
giúp mình vs ạ
\(Cho A=\left (\frac{2-\sqrt[3]{4x}}{x-\sqrt[3]{2x^2}} \right ):\left ( \sqrt[3]{2}+\sqrt[3]{x} \right )-\frac{1}{\sqrt[3]{x}}\) với \(x\ne0,-2\)
Tìm \(x\in Z \) để \(A ^3 \in Z\)
\(A=\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2}{\sqrt{x}+1}-\dfrac{2}{x-1}\)
a) Rg A
b) Tính A khi x=9; x=7-\(4\sqrt{3}\)
c) Tìm x ϵ Z để A có giá trị nguyên
d) Tìm x để A=\(\dfrac{1}{\sqrt{x}}\); A=-2
Giải Phương trình
a) \(\sqrt{4x-4}\) = \(\dfrac{x+3}{2}\)
b) x+y+z+8= \(2\sqrt{x-1}+4\sqrt{y-2}+6\sqrt{z-3}\)
tìm max:
a, \(A=3\sqrt{2x-1}+x\sqrt{5-4x^2}\) với 1/2<=x<= căn 5/2
b, \(B=\frac{xyz\left(x+y+z+\sqrt{x^2+y^2+z^2}\right)}{\left(x^2+y^2+z^2\right)\left(xy+yz+zx\right)};x,y,z>0\)
Tìm X biết
a) √x+1 = x-1
b) √1-x + √4+x =3
C) x+y+z+4 = 2×√x-2 + 4×√y-3 + 6×√z-5
d) √x^2 -2x+1 + √x^2 +4x +4 =3
e) √x+3+4√x-1 + √x+8-6√x-1
F) √6-x + √x-2 = x^2 -6x + 13
a.tìm a+b+c=2\(\sqrt{a}+2\sqrt{b-3}+2\sqrt{c}\)
b.tìm x,y,z thỏa mãn x+y+z+8=2\(\sqrt{x-1}+4\sqrt{y-2}+6\sqrt{z-3}\)