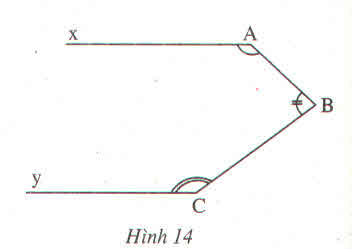
kéo dài BC cắt xx' tại G
có góc yCB = 125o mà yCB và yCG là hai góc kề bù
=> yCG = 55o (1)
tam giác ABG có xAB = 70o
GBA = 55o
=> AGC = 55o (2)
có AGC và yCG là 2 góc ở vị trí so le trong (3)
từ 1 ,2và 3 =>xx'//Cy
Giải :
ta có : \(\widehat{xAB}\) + \(\widehat{BAx'}\) = \(180^0\) ( 2 góc kề bù )
thay vào ta có : \(70^0\) + \(\widehat{BAx'}\) = \(180^0\)
=> \(\widehat{BAx'}\) = \(110^0\)
ta lại có : Am là tia phân giác của \(\widehat{BAx'}\)
=> \(\widehat{BAm}\) = \(\widehat{mAx'}\) = \(\widehat{BAx'}\) : 2
=> \(\widehat{BAm}\) = \(\widehat{mAx'}\) = \(110^0\) : 2 = \(55^0\)
=> \(\widehat{BAm}\) = \(55^0\) = \(\widehat{CBA}\) => ( 2 góc so le trong )
vậy Am // BC (đpcm).
b) có xAB và và BAx' là 2 góc kề bù
mà xAB = 70o => BAx' = 110o
có AM là tia pg của BAx' =>BAM =55o (4)
Lại có ABC = 55o (5)
ABC VÀ BAM ở vị trí so le trong (6)
từ 4,5 và 6 =>AM // BC