1. Cho tam giác ABC, tia phân giác góc B cắt AC tại góc D. Trên tia đối của tia BA lấy điểm E sao cho BE= BC. Chứng minh BD//EC.
2. Chi tam giác ABC, các tia phân giác góc B, góc C cắt nhau ở I . Qua I kẻ đường thẳng song song vs BC. Đường thẳng này cắt AB, AC theo thứ tự góc D và góc E. Chứng minh DE=BD+CE.
3. Chi tam giác đều ABC trên cạnh AB, BC,CA lấy lần lượt các điểm M,N,P sao cho AM=BN. Chứng minh tan giác MNP đều
Bài 1:
+ Xét \(\Delta BCE\) có:
\(BE=BC\left(gt\right)\)
=> \(\Delta BCE\) cân tại B.
=> \(\widehat{BEC}=\widehat{BCE}\) (tính chất tam giác cân)
+ Vì \(\widehat{ABC}\) là góc ngoài tại đỉnh B của \(\Delta BCE.\)
=> \(\widehat{BEC}+\widehat{BCE}=\widehat{ABC}\) (tính chất góc ngoài của tam giác)
Mà \(\widehat{BEC}=\widehat{BCE}\left(cmt\right)\)
=> \(2\widehat{BEC}=\widehat{ABC}\) (1).
+ Vì \(BD\) là tia phân giác của \(\widehat{B}\left(gt\right)\)
=> \(\widehat{ABD}=\widehat{CBD}=\frac{1}{2}\widehat{ABC}.\)
Hay \(\widehat{ABC}=2\widehat{ABD}\) (2).
Từ (1) và (2) => \(\widehat{2ABD}=2\widehat{BEC}\)
=> \(\widehat{ABD}=\widehat{BEC}.\)
Mà 2 góc này nằm ở vị trí đồng vị.
=> \(BD\) // \(EC\left(đpcm\right).\)
Chúc bạn học tốt!
Bài 2:
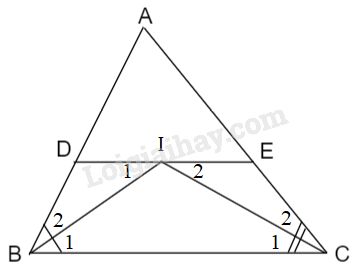
+ Vì \(DI\) // \(BC\left(gt\right)\)
=> \(\widehat{I_1}=\widehat{B_1}\) (vì 2 góc so le trong) (1).
+ Vì \(BI\) là tia phân giác của \(\widehat{B}\left(gt\right)\)
=> \(\widehat{B_1}=\widehat{B_2}\) (2).
Từ (1) và (2) => \(\widehat{I_1}=\widehat{B_2}.\)
=> \(\Delta BDI\) cân tại D.
=> \(BD=DI\) (tính chất tam giác cân) (3).
+ Vì \(IE\) // \(BC\left(gt\right)\)
=> \(\widehat{I_2}=\widehat{C_1}\) (vì 2 góc so le trong) (4).
+ Vì \(CI\) là tia phân giác của \(\widehat{C}\left(gt\right)\)
=> \(\widehat{C_1}=\widehat{C_2}\) (5).
Từ (4) và (5) => \(\widehat{I_2}=\widehat{C_2}.\)
=> \(\Delta CEI\) cân tại E.
=> \(CE=EI\) (tính chất tam giác cân) (6).
Từ (3) và (6) => \(BD+CE=DI+EI.\)
Mà \(DI+EI=DE.\)
=> \(BD+CE=DE\)
Hay \(DE=BD+CE\left(đpcm\right).\)
Chúc bạn học tốt!
Bài 1.
Ta có: $BE=BC$ nên $\Delta BEC$ cân
$\Rightarrow \widehat{E}=\widehat{BCE}$
$\widehat{ABC}$ là góc ngoài của $\Delta BEC$ nên $\widehat{ABC}=\widehat{E}+\widehat{BCE}=2\widehat{E}$
Mà $\widehat{ABD}=\widehat{DBC}$
$\Rightarrow \widehat{E}=\widehat{BCE}=\widehat{ABD}=\widehat{DBC}$
$\Rightarrow DB//CE$
Bài 2.
Vì $DE // BC$ nên \(\widehat{DIB}\) = \(\widehat{IBC}\) ( so le trong)
mà \(\widehat{DBI}\) = \(\widehat{IBC}\) \(\Rightarrow\) \(\widehat{DIB}\) = \(\widehat{DBI}\)
\(\Rightarrow\) \(\Delta\)DIB cân tại $D$
\(\Rightarrow\) $BD = DI (1)$
Lại vì $DE // BC$ nên \(\widehat{EIC}\) = \(\widehat{ICB}\) (so le trong)
mà \(\widehat{ECI}\) = \(\widehat{ICB}\) \(\Rightarrow\) \(\widehat{EIC}\) = \(\widehat{ECI}\)
\(\Rightarrow\) \(\Delta\)EIC cân tại E
\(\Rightarrow\) $CE = IE (2)$
Ta có: $DE = DI + IE (3)$
Thay (1); (2) vào (3) ta được:
$DE = BD + CE$ \(\rightarrow\) đpcm.














