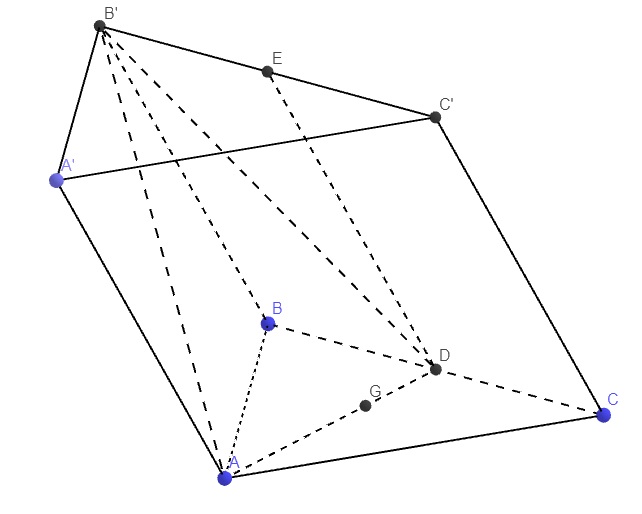
Gọi D là trung điểm BC và E là trung điểm B'C' \(\Rightarrow DE||B'B||C'C||A'A\)
\(\Rightarrow\)4 điểm A',A,D,E đồng phẳng
Đồng thời ABC là tam giác đều \(\Rightarrow AD\perp BC\) và G thuộc AD
Hai tam giác A'AB và A'AC có \(A'A\) chung, \(\widehat{A'AB}=\widehat{A'AC}=120^0\) và \(AB=AC=a\)
\(\Rightarrow\Delta A'AB=\Delta A'AC\left(c.g.c\right)\Rightarrow A'B=A'C\)
\(\Rightarrow\Delta A'BC\) cân tại A' \(\Rightarrow A'D\) là trung tuyến đồng thời là đường cao
\(\Rightarrow BC\perp A'D\)
\(\Rightarrow BC\perp\left(A'ADE\right)\) \(\Rightarrow BC\perp DE\Rightarrow BC\perp B'B\)
\(\Rightarrow B'BCC'\) là hình chữ nhật hay tam giác B'BD vuông tại B
Pitago: \(B'D=\sqrt{B'B^2+BD^2}=\sqrt{\left(2a\right)^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{17}}{2}\)
\(AD=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\widehat{ABB'}=180^0-\widehat{A'AB}=60^0\) (2 góc trong cùng phía)
Định lý hàm cosin trong tam giác ABB':
\(B'A=\sqrt{AB^2+B'B^2-2AB.B'B.cos\widehat{ABB'}}=a\sqrt{3}\)
Định lý hàm cosin trong tam giác AB'D:
\(cos\widehat{GAB'}=\dfrac{B'A^2+AD^2-B'D^2}{2B'A.AD}=-\dfrac{1}{6}\)
\(\Rightarrow\widehat{GAB'}\approx99^035'\)