Bài 4:
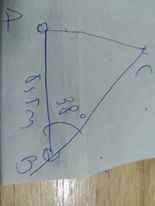
1: Gọi AC là chiều cao của cột đèn, AB là bóng của cột đèn trên mặt đất
=>AB\(\perp\)AC tại A
Theo đề, ta có: AB=8,5m và \(\widehat{B}=38^0\)
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}\)
=>\(AC=AB\cdot tanB=8,5\cdot tan38\simeq6,6\left(m\right)\)
Câu 2:
a: ΔAHC vuông tại H
=>\(AH^2+HC^2=AC^2\)
=>\(HC^2+3^2=5^2\)
=>\(HC^2=5^2-3^2=16\)
=>HC=4(cm)
Xét ΔCAD vuông tại C có CH là đường cao
nên \(CH^2=HA\cdot HD\)
=>HD*3=16
=>HD=16/3(cm)
AD=AH+HD
=3+16/3
=25/3(cm)
Xét ΔADC vuông tại C có CH là đường cao
nên \(DC^2=DH\cdot DA\)
=>\(DC^2=\dfrac{16}{3}\cdot\dfrac{25}{3}=\dfrac{400}{9}\)
=>\(DC=\dfrac{20}{3}\left(cm\right)\)
b: ΔCHD vuông tại H có HF là đường cao
nên \(CF\cdot CD=CH^2\left(1\right)\)
ΔCHA vuông tại H có HE là đường cao
nên \(CE\cdot CA=CH^2\left(2\right)\)
Từ (1) và (2) suy ra \(CF\cdot CD=CE\cdot CA\)























