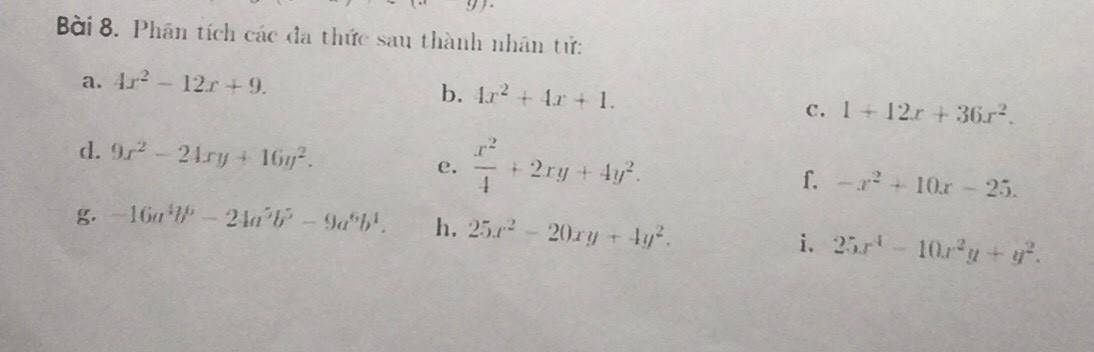\(a,4x^2-12x+9=4\left(x^2-3x+\dfrac{9}{4}\right)\\ =4\left(x^2-2.x.\dfrac{3}{2}+\dfrac{3^2}{2^2}\right)=4\left(x-\dfrac{3}{2}\right)^2\\ b,4x^2+4x+1=\left(2x\right)^2+2.2x.1+1^2=\left(2x+1\right)^2\\ c,1+12x+36x^2=1^2+2.1.6x+\left(6x\right)^2=\left(1+6x\right)^2\\ d,9x^2-24xy+16y^2=\left(3x\right)^2-2.3x.4y+\left(4y\right)^2\\ =\left(3x-4y\right)^2\\ e,\dfrac{x^2}{4}+2xy+4y^2=\left(\dfrac{1}{2}x\right)^2+2.\dfrac{1}{2}x.2y+\left(2y\right)^2\\ =\left(\dfrac{1}{2}x+2y\right)^2\)
\(f,-x^2+10x-25=-\left(x^2-10x+25\right)\\ =-\left(x^2-2.x.5+5^2\right)=-\left(x-5\right)^2\\ g,-16a^4b^6-24a^5b^5-9a^6b^4=-\left(16a^4b^6+24a^5b^5+9a^6b^4\right)\\ =-\left[\left(4a^2b^3\right)^2+2.4a^2b^3.3a^3b^2+\left(3a^3b^2\right)^2\right]=-\left(4a^2b^3+3a^3b^2\right)^2\\ h,25x^2-20xy+4y^2=\left(5x\right)^2-2.5x.2y+\left(2y\right)^2=\left(5x-2y\right)^2\\ i,25x^4-10x^2y+y^2=\left(5x^2\right)^2-2.5x^2y+y^2=\left(5x^2-y\right)^2\)