a) ĐK: a>0
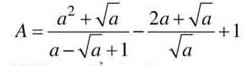
\(=\dfrac{\sqrt{a}[\left(\sqrt{a}\right)^3+1]}{a-\sqrt{a}+1}-\dfrac{\sqrt{a}\left(2\sqrt{a}+1\right)}{\sqrt{a}}+1\)
\(=\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{a-\sqrt{a}+1}-2\sqrt{a}-1+1\)
\(=a+\sqrt{a}-2\sqrt{a}\)
\(=a-\sqrt{a}\)
b) \(A=2\Leftrightarrow a-\sqrt{a}=2\Leftrightarrow a-\sqrt{a}-2=0\)
\(\Leftrightarrow(\sqrt{a}+1)\left(\sqrt{a}-2\right)=0\)
\(\Leftrightarrow\sqrt{a}-2=0\) (vì \(\sqrt{a}+1>0\) )
\(\Leftrightarrow\sqrt{a}=2\Leftrightarrow a=4\) (t/m)
a: \(A=\dfrac{\sqrt{a}\left(a\sqrt{a}+1\right)}{a-\sqrt{a}+1}-2\sqrt{a}-1+1\)
\(=a+\sqrt{a}-2\sqrt{a}=a-\sqrt{a}\)
b: A=2
=>a-căn a-2=0
=>(căn a-2)(căn a+1)=0
=>căn a-2=0
=>a=4
















