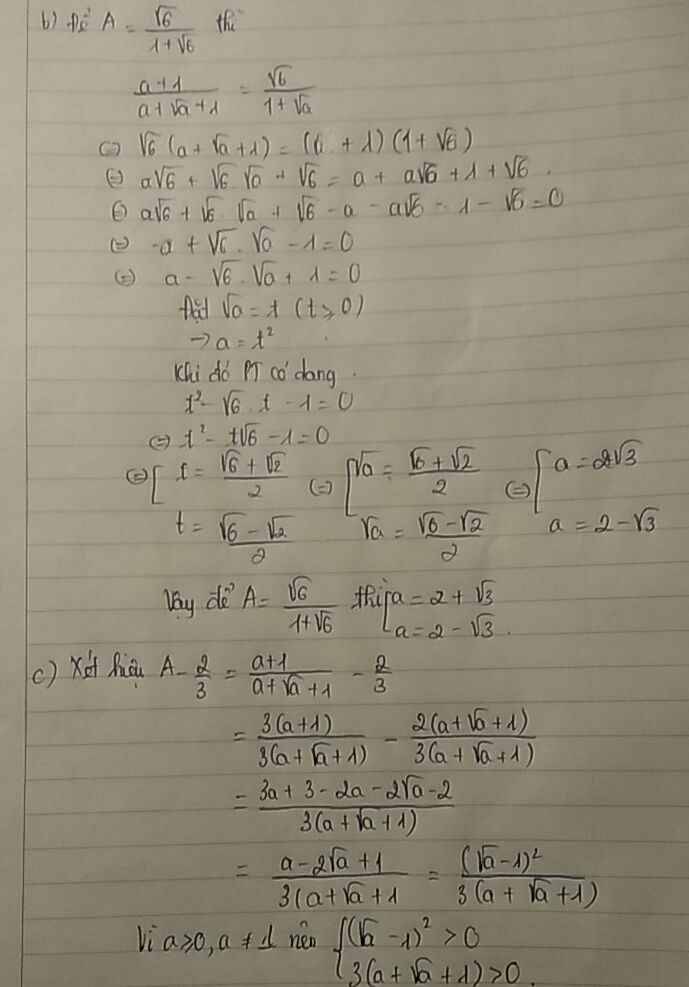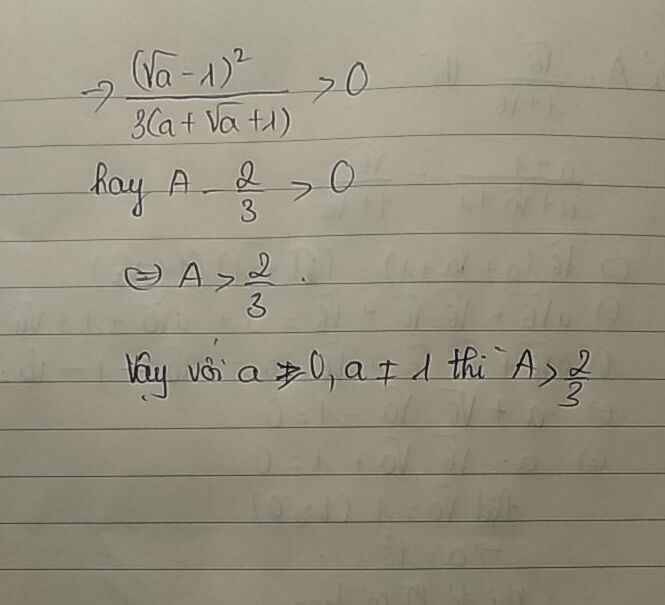a: Đặt \(B=\dfrac{2a+\sqrt{a}-1}{1-a}-\dfrac{2a\sqrt{a}-\sqrt{a}+a}{1-a\sqrt{a}}\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(2\sqrt{a}-1\right)}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}+\dfrac{\sqrt{a}\left(2a+\sqrt{a}-1\right)}{a\sqrt{a}-1}\)
\(=\dfrac{\left(-2\sqrt{a}+1\right)\left(a+\sqrt{a}+1\right)+2a\sqrt{a}+a-\sqrt{a}}{a\sqrt{a}-1}\)
\(=\dfrac{-2a\sqrt{a}-a-\sqrt{a}+1+2a\sqrt{a}+a-\sqrt{a}}{a\sqrt{a}-1}\)
\(=\dfrac{-2\sqrt{a}+1}{a\sqrt{a}-1}\)
\(A=1+\dfrac{-2\sqrt{a}+1}{a\sqrt{a}-1}\cdot\dfrac{a-\sqrt{a}}{2\sqrt{a}-1}\)
\(=1-\dfrac{\sqrt{a}}{a+\sqrt{a}+1}=\dfrac{a+1}{a+\sqrt{a}+1}\)
c: \(A-\dfrac{2}{3}=\dfrac{a+1}{a+\sqrt{a}+1}-\dfrac{2}{3}\)
\(=\dfrac{3a+3-2a-2\sqrt{a}-2}{3\left(a+\sqrt{a}+1\right)}=\dfrac{\left(\sqrt{a}-1\right)^2}{3\left(a+\sqrt{a}+1\right)}>0\)
=>A>2/3