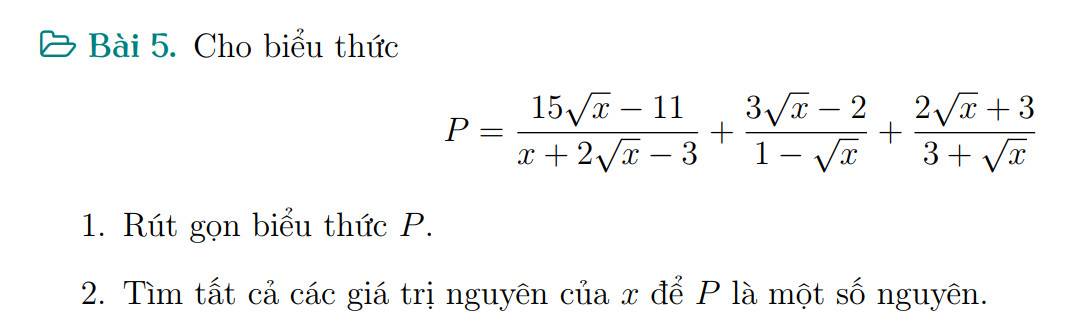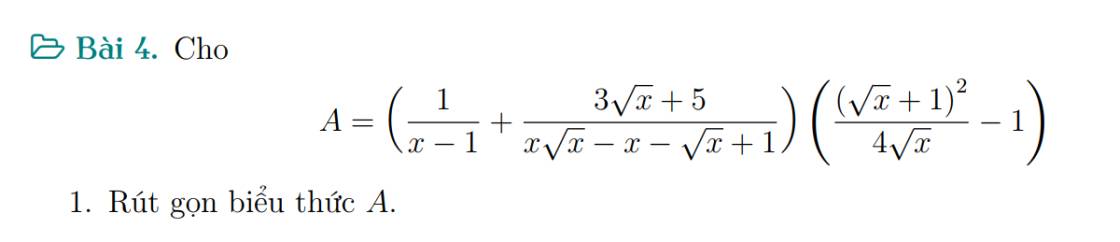Bài 4:
Với \(x>0;x\ne1\)
\(A=\left[\dfrac{1}{x-1}+\dfrac{3\sqrt{x}+5}{x\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)}\right].\dfrac{x+2\sqrt{x}+1-4\sqrt{x}}{4\sqrt{x}}\\ =\left[\dfrac{1}{x-1}+\dfrac{3\sqrt{x}+5}{\left(x-1\right)\left(\sqrt{x-1}\right)}\right].\dfrac{x-2\sqrt{x}+1}{4\sqrt{x}}\\ =\dfrac{\sqrt{x}-1+3\sqrt{x}+5}{\left(x-1\right)\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{4\sqrt{x}}\\ =\dfrac{4\sqrt{x}+4}{\left(\sqrt{x}+1\right)4\sqrt{x}}=\dfrac{4\left(\sqrt{x}+1\right)}{4\sqrt{x}\left(\sqrt{x}+1\right)}=\dfrac{1}{\sqrt{x}}\)
5:
1: \(P=\dfrac{15\sqrt{x}-11-\left(3\sqrt{x}-2\right)\left(\sqrt{x}+3\right)+\left(2\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{15\sqrt{x}-11-3x-7\sqrt{x}+6+2x+\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-x+9\sqrt{x}-8}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}=\dfrac{-\sqrt{x}+8}{\sqrt{x}+3}\)
2: P nguyên
=>-căn x-3+11 chia hết cho căn x+3
=>căn x+3=11
=>căn x=8
=>x=64