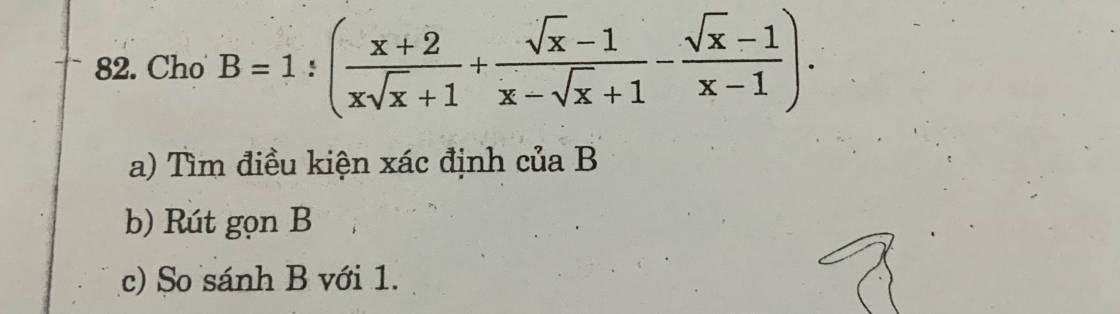`(a):ĐKXĐ:x>0;x\ne1`
`(b):B=1:((x+2)/(x\sqrt{x}+1)+(\sqrt{x}-1)/(x-\sqrt{x}+1)-(\sqrt{x}-1)/(x-1))`
`=1:((x+2)/((\sqrt{x}+1)(x-\sqrt{x}+1)+(\sqrt{x}-1)/(x-\sqrt{x}+1)-(1)/(\sqrt{x}+1))`
`=1:(x+2+(\sqrt{x}-1)(\sqrt{x}+1)-(x-\sqrt{x}+1))/((\sqrt{x}+1)(x-\sqrt{x}+1))`
`=1:(x+2+x-1-x+\sqrt{x}-1)/((\sqrt{x}+1)(x-\sqrt{x}+1)`
`=1.((\sqrt{x}+1)(x-\sqrt{x}+1))/(x+\sqrt{x})`
`=((\sqrt{x}+1)(x-\sqrt{x}+1))/(\sqrt{x}(\sqrt{x}+1))`
`=(x-\sqrt{x}+1)/(\sqrt{x})`
`(c):B-1=(x-\sqrt{x}+1)/(\sqrt{x})-1`
`=(x-\sqrt{x}+1-\sqrt{x})/(\sqrt{x})`
`=((\sqrt{x}-1)^{2})/(\sqrt{x})`
Với `x>0;x\ne1=>(\sqrt{x}-1)^{2}>0;\sqrt{x}>0`
`=>B-1=((\sqrt{x}-1)^{2})/(\sqrt{x})>0`
Hay `B>1`
a: ĐKXĐ: x>=0; x<>1
b: \(B=1:\left(\dfrac{x+2+x-1-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x+\sqrt{x}}=\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\)
c: \(B-1=\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}>0\)
=>B>1