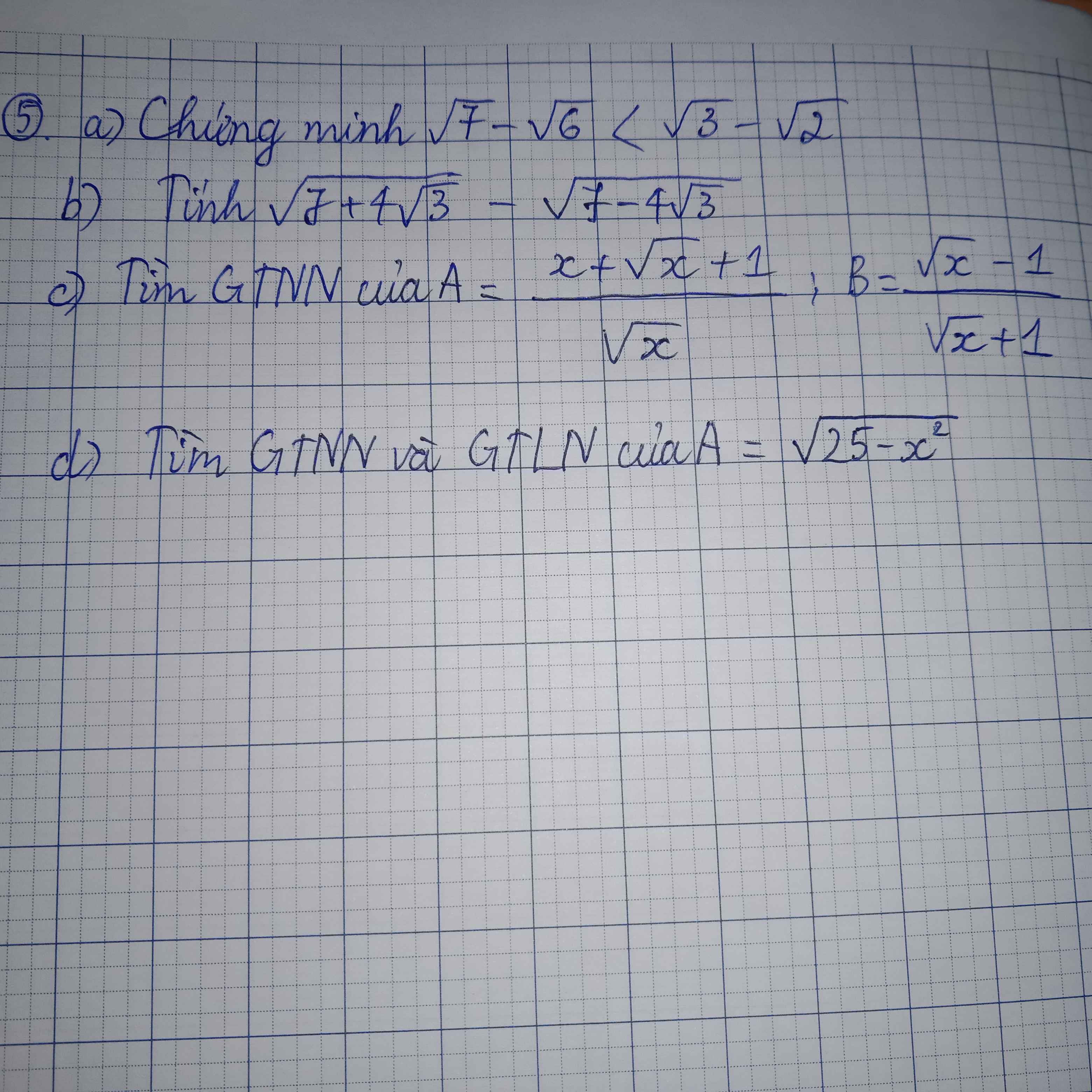a) \(\sqrt{7}-\sqrt{6}=\dfrac{1}{\sqrt{7}+\sqrt{6}}< \dfrac{1}{\sqrt{3}+\sqrt{2}}=\sqrt{3}-\sqrt{2}\) ( đpcm )
b) \(\sqrt{7+4\sqrt{3}}-\sqrt{7-4\sqrt{3}}\) = \(\sqrt{\left(2+\sqrt{3}\right)^2}-\sqrt{\left(2-\sqrt{3}\right)^2}\)
\(=2+\sqrt{3}-\left(2-\sqrt{3}\right)=2\sqrt{3}\)
c) ĐKXĐ : x > 0
Ta có : \(A=\dfrac{x+1+\sqrt{x}}{\sqrt{x}}=\sqrt{x}+\dfrac{1}{\sqrt{x}}+1\ge2+1=3\) ( BĐT Cô - si )
' = ' \(\Leftrightarrow x=1\)
ĐKXĐ : x \(\ge0\)\(;B=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=1-\dfrac{2}{\sqrt{x}+1}\ge1-2=-1\) . " = " \(\Leftrightarrow x=0\)
d) ĐKXĐ : \(-5\le x\le5\)
\(A=\sqrt{25-x^2}\ge0\) . " = " \(\Leftrightarrow x=\pm5\)
\(A\le5\) . " = " \(\Leftrightarrow x=0\)