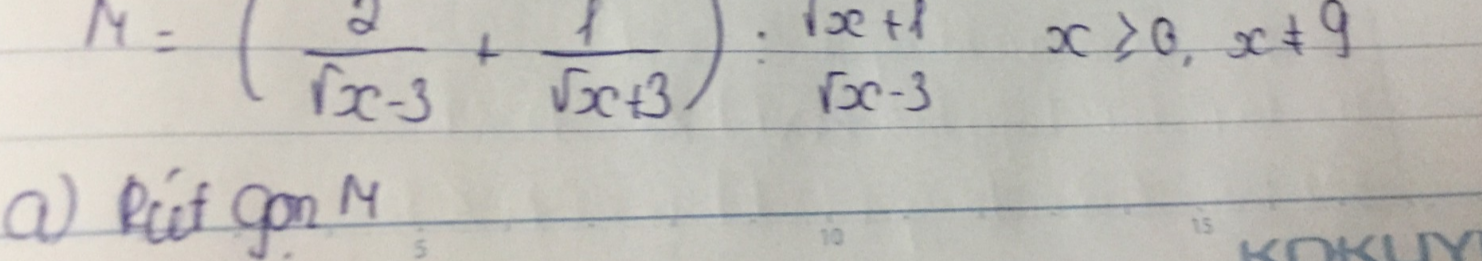ĐK: \(x\ge0;x\ne9\)
a) \(M=\left(\dfrac{2}{\sqrt{x}-3}+\dfrac{1}{\sqrt{x}+3}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\dfrac{2\left(\sqrt{x}+3\right)+\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ =\dfrac{3\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ =\dfrac{3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\\ =\dfrac{3}{\sqrt{x}+3}\)
b) \(M=\dfrac{\sqrt{x}}{6}\Leftrightarrow\dfrac{3}{\sqrt{x}+3}=\dfrac{\sqrt{x}}{6}\Leftrightarrow\sqrt{x}\left(\sqrt{x}+3\right)=18\)
\(\Leftrightarrow x+3\sqrt{x}-18=0\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=3\Leftrightarrow x=9\left(L\right)\\\sqrt{x}=-6\left(L\right)\end{matrix}\right.\)
Vậy không có x thỏa mãn.
c) \(2M>1\Leftrightarrow\dfrac{6}{\sqrt{x}+3}>1\Leftrightarrow6>\sqrt{x}+3\Leftrightarrow\sqrt{x}< 3\Leftrightarrow x< 9\)
Mà \(x\) nguyên, \(x\ge0;x\ne9\) nên ta có các giá trị thỏa mãn là:
\(x\in\left\{0;1;2;...;8\right\}\)
d) Do \(\sqrt{x}\ge0\Rightarrow\sqrt{x}+3\ge3\Rightarrow M\le\dfrac{3}{3}=1\)
Dấu = xảy ra \(\Leftrightarrow x=0\) (TM)
Vậy \(M_{max}=1\) đạt được khi \(x=0\)