\(Q=\Sigma\dfrac{x}{1+y^2}+\dfrac{3}{2}xyz=\Sigma\dfrac{x}{1+y^2}+\dfrac{xy+yz+xz}{2}=x+y+z-\left(\dfrac{xy^2}{1+y^2}+\dfrac{yz^2}{1+z^2}+\dfrac{zx^2}{1+x^2}\right)+\dfrac{xy+yz+xz}{2}\)
\(có:xy+yz+xz=3xyz\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{x}=3\ge\dfrac{9}{x+y+z}\Leftrightarrow x+y+z\ge3\)
\(\Rightarrow Q\ge3-\left(\dfrac{xy+yz+xz}{2}\right)+\dfrac{xy+yz+xz}{2}=3\)
\(dấu"="\Leftrightarrow x=y=z=1\)
Đúng 0
Bình luận (0)
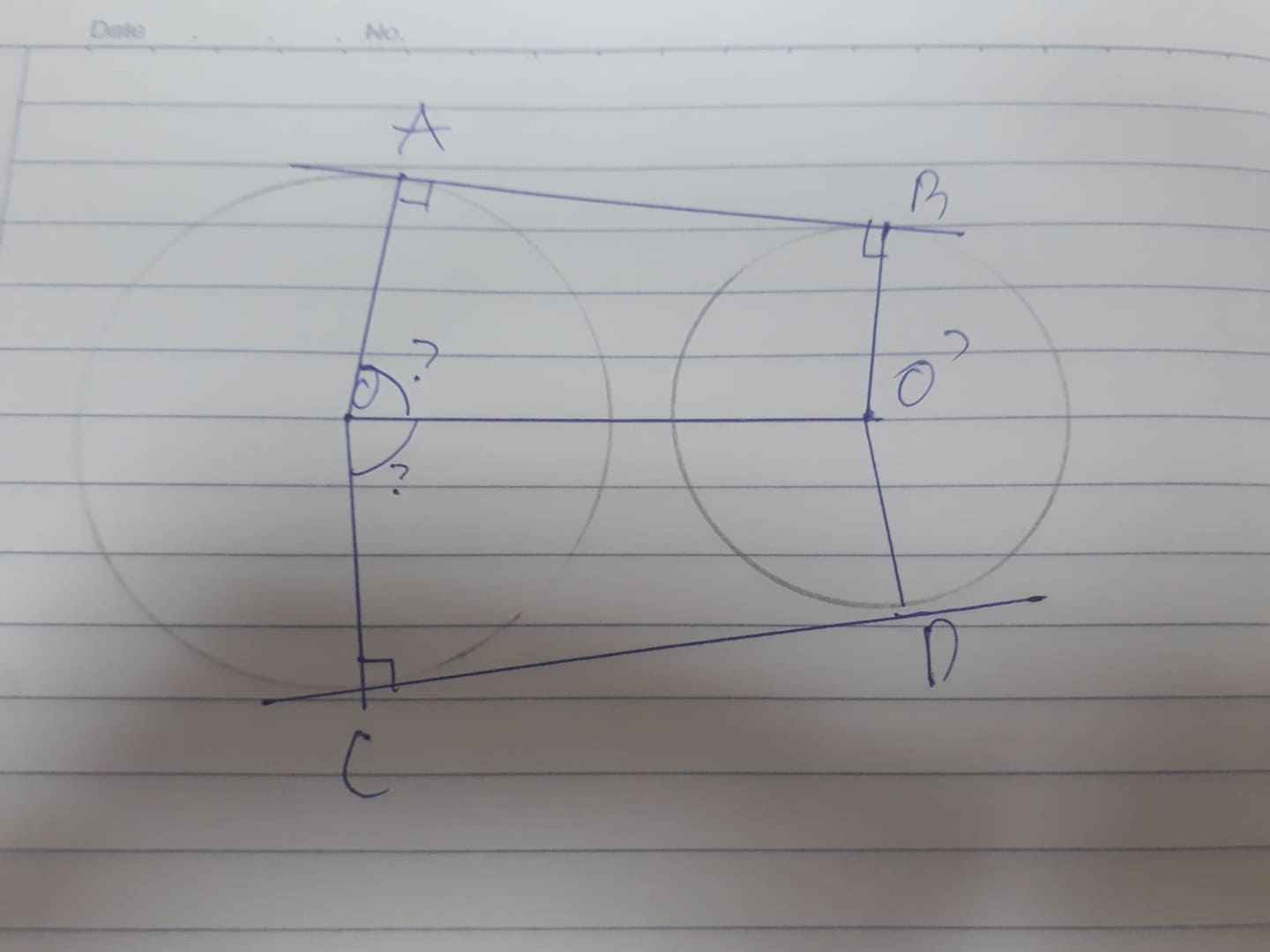ai chứng minh hộ mik 2 góc ? trên kia bằng nhau hô j mik với
