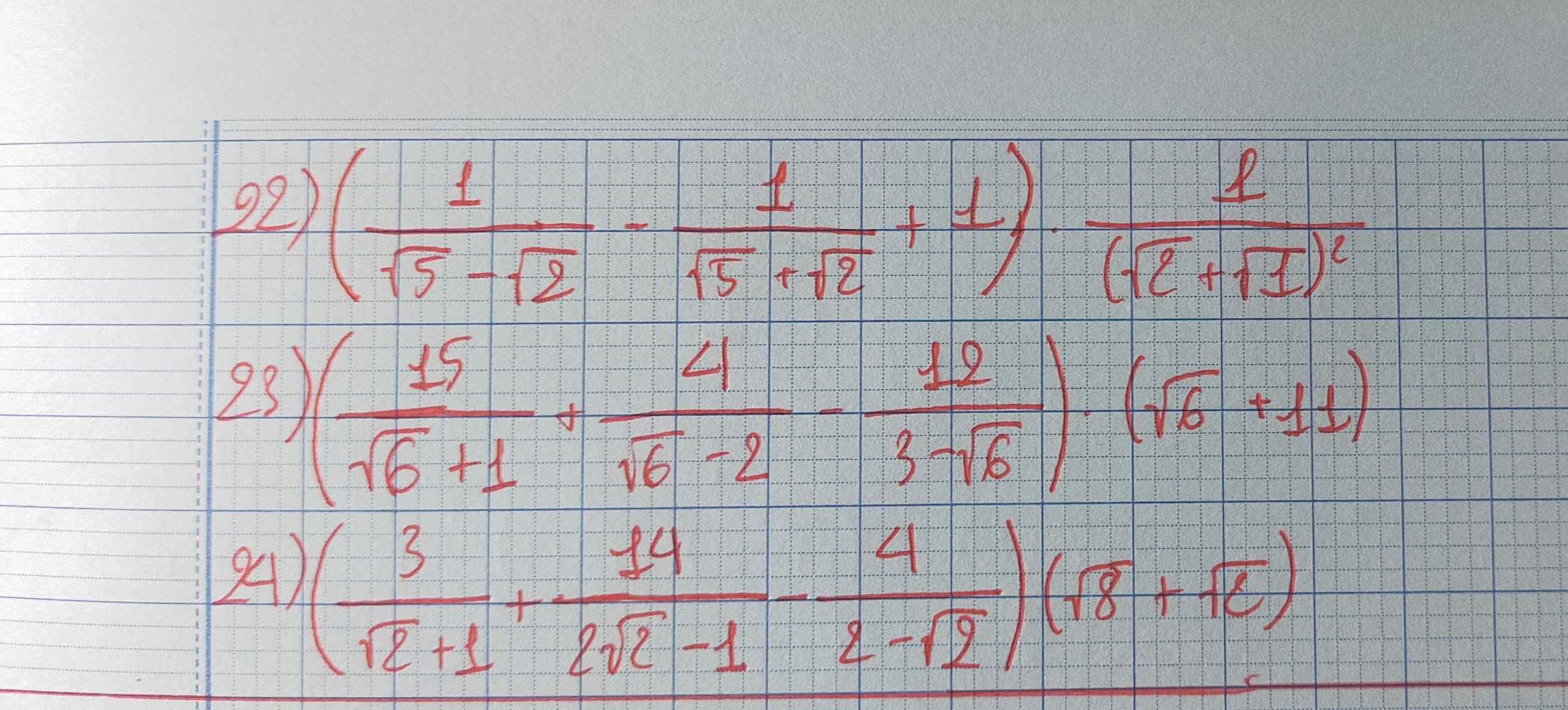22: \(=\dfrac{\sqrt{5}+\sqrt{2}-\sqrt{5}+\sqrt{2}+3}{3}\cdot\dfrac{1}{3+2\sqrt{2}}\)
\(=\dfrac{3+2\sqrt{2}}{3+2\sqrt{2}}\cdot\dfrac{1}{3}=\dfrac{1}{3}\)
23: \(=\left(\dfrac{15\left(\sqrt{6}-1\right)}{5}+\dfrac{4\left(\sqrt{6}+2\right)}{2}-\dfrac{12\left(3+\sqrt{6}\right)}{3}\right)\cdot\left(11+\sqrt{6}\right)\)
\(=\left(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}\right)\cdot\left(\sqrt{6}+11\right)\)
\(=\left(\sqrt{6}-11\right)\left(\sqrt{6}+11\right)\)
=6-121=-115
Đúng 1
Bình luận (0)
