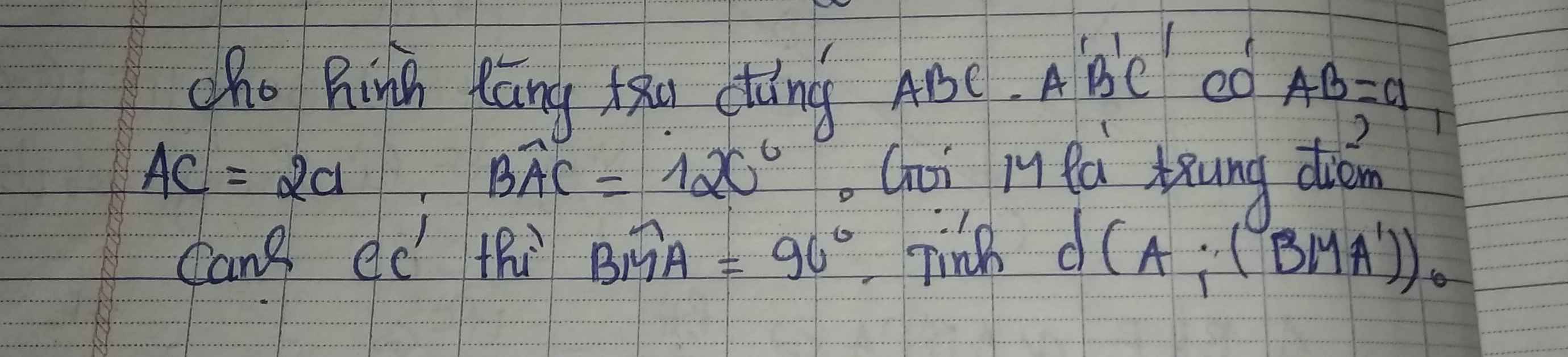\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow\left(SBC\right)\perp\left(SAB\right)\)
\(SA\perp\left(ABCD\right)\Rightarrow\left(SAB\right)\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{SBA}\) là góc giữa (SBCD) và (ABCD)
\(\Rightarrow\widehat{SBA}=60^0\)
\(\Rightarrow SA=AB.tan60^0=a\sqrt{3}\)
1. Chắc là đề sai, vì BC và AC cắt nhau tại C nên \(d\left(BC,AC\right)=0\)
2. Gọi G là giao điểm AC và BD
Talet: \(\dfrac{CG}{AG}=\dfrac{BC}{AD}=\dfrac{1}{2}\Rightarrow CG=\dfrac{1}{2}AG\Rightarrow CG=\dfrac{1}{3}AC\)
Qua C kẻ đường thẳng song song BD cắt AB kéo dài tại E
\(\Rightarrow BD||\left(SCE\right)\Rightarrow d\left(BD;SC\right)=d\left(BD;\left(SCE\right)\right)=d\left(G;\left(SCE\right)\right)\)
Do \(\left\{{}\begin{matrix}AG\cap\left(SCE\right)=C\\GC=\dfrac{1}{3}AC\end{matrix}\right.\) \(\Rightarrow d\left(G;\left(SCE\right)\right)=\dfrac{1}{3}d\left(A;\left(SCE\right)\right)\)
Từ A dựng \(AH\perp CE\) , dựng \(AK\perp SH\Rightarrow AK\perp\left(SCE\right)\)
\(\Rightarrow AK=d\left(A;\left(SCE\right)\right)\)
\(\widehat{EAH}=\widehat{BCE}\) (cùng phụ \(\widehat{AEH}\)) ; \(\widehat{BCE}=\widehat{ADB}\) (góc có cạnh tương ứng song song)
\(BE=BC.tan\widehat{BCE}=BC.tan\widehat{ADB}=BC.\dfrac{AB}{AD}=\dfrac{a}{2}\) \(\Rightarrow AE=\dfrac{3a}{2}\)
\(\Rightarrow AH=AE.cos\widehat{EAH}=AE.cos\widehat{ADB}=AE.\dfrac{AD}{\sqrt{AB^2+AD^2}}=\dfrac{3a\sqrt{5}}{5}\)
Hệ thức lượng: \(AK=\dfrac{SA.AH}{\sqrt{SA^2+AH^2}}=\dfrac{3a\sqrt{2}}{4}\)
\(\Rightarrow d\left(SC;BD\right)=\dfrac{1}{3}AK=\dfrac{a\sqrt{2}}{4}\)