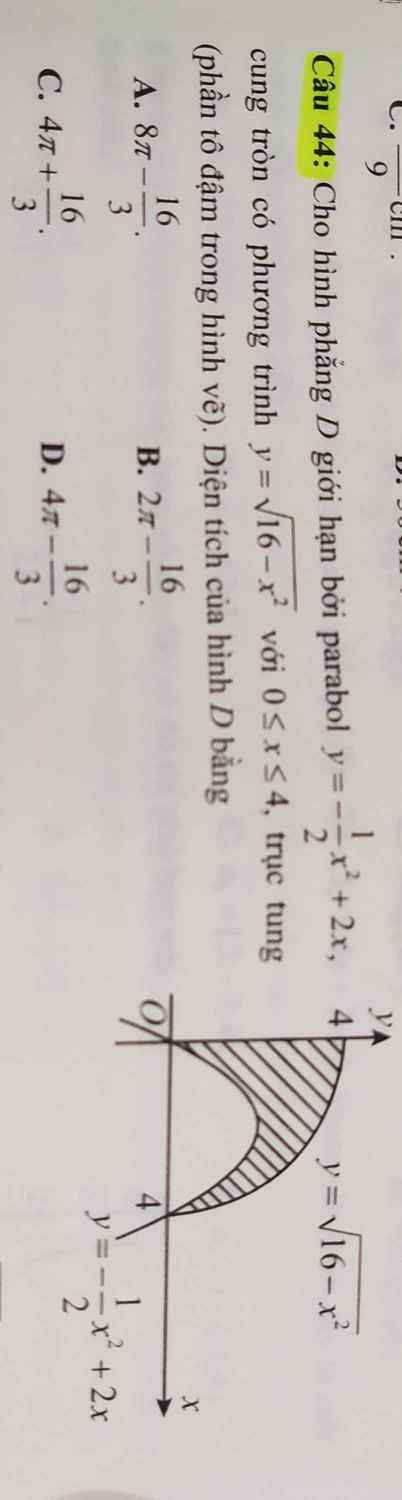Diện tích của hình D bằng: \(\int_0^4\sqrt{16-x^2}dx-\int_0^4\left(-\dfrac{1}{2}x^2+2x\right)dx\)\(=4\pi-\dfrac{16}{3}\)
Đáp án D
Diện tích phần tô đậm bằng (diện tích giới hạn bởi cung tròn \(y=\sqrt{16-x^2}\) ; trục Ox, trục Oy) - (diện tích giới hạn bởi parabol \(y=-\dfrac{1}{2}x^2+2x\) và trục Ox)
\(\Rightarrow S=\int\limits^4_0\sqrt{16-x^2}dx-\int\limits^4_0\left(-\dfrac{1}{2}x^2+2x\right)dx\)
Xét \(\int\limits^4_0\sqrt{16-x^2}dx\) (thực chất nó là 1/4 hình tròn có bán kính bằng 4 nên tính nhanh được \(S=\dfrac{1}{4}.\pi.4^2=4\pi\) mà ko cần tích phân)
Đặt \(x=4sint\Rightarrow dx=4cost.dt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=0\\x=4\Rightarrow t=\dfrac{\pi}{2}\end{matrix}\right.\)
\(I=\int\limits^{\dfrac{\pi}{2}}_0\sqrt{16-16sin^2t}.4cost.dt=16\int\limits^{\dfrac{\pi}{2}}_0cos^2tdt=8\int\limits^{\dfrac{\pi}{2}}_0\left(1+cos2t\right)dt\)
\(=8\left(x+\dfrac{1}{2}sin2t\right)|^{\dfrac{\pi}{2}}_0=4\pi\)
Còn \(\int\limits^4_0\left(-\dfrac{1}{2}x^2+2x\right)dx=\dfrac{16}{3}\) là tích phân cơ bản (bấm máy là được rồi)