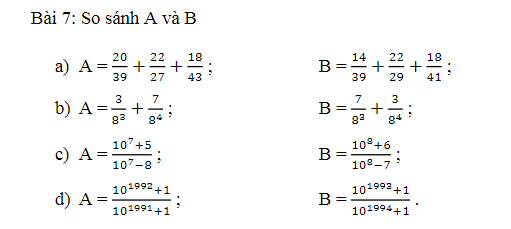Lời giải:
a.
\(A-B=\frac{20-14}{39}+(\frac{22}{27}-\frac{22}{29})+(\frac{18}{43}-\frac{18}{41})\)
\(=\frac{6}{39}+22.\frac{2}{27.29}+\frac{18.(-2)}{43.41}=\frac{6}{39}+\frac{44}{27.29}-\frac{36}{43.41}\)
Dễ thấy $\frac{44}{27.29}> \frac{36}{43.41}; \frac{6}{39}>0$ nên $A-B>0$
$\Rightarrow A>B$
b.
\(A-B=\frac{3-7}{8^3}+\frac{7-3}{8^4}=\frac{4}{8^4}-\frac{4}{8^3}=\frac{4(8^3-8^4)}{8^3.8^4}<0\Rightarrow A< B\)
c.
\(A-1=\frac{13}{10^7-8}; B-1=\frac{13}{10^8-7}\)
Mà \(10^7-8-(10^8-7)=10^7-10^8-1<0\Rightarrow 10^7-8< 10^8-7\Rightarrow A-1> B-1\)
$\Rightarrow A>B$
d.
\(A=\frac{10^{1992}+1}{10^{1991}+1}>\frac{10^{1991}+1}{10^{1991}+1}=1; B=\frac{10^{1993}+1}{10^{1994}+1}<\frac{10^{1993}+1}{10^{1993}+1}=1\)
$\Rightarrow A>B$