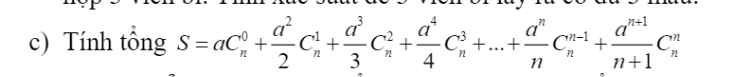Question

Answer 1

Lời giải:
Ta thấy:
\(\frac{C^k_n}{k+1}=\frac{n!}{k!(n-k)!(k+1)}=\frac{n!}{(k+1)!(n-k)!}\)

\(\Rightarrow \frac{n+1}{k+1}C^k_n=C^{k+1}_{n+1}\)

Do đó:

\(S(n+1)=aC^1_{n+1}+a^2C^2_{n+1}+a^3C^3_{n+1}+....+a^{n+1}C^{n+1}_{n+1}\)

\(=a^0C^0_{n+1}+a^1C^1_{n+1}+..+a^{n+1}C^{n+1}_{n+1}-1=(a+1)^{n+1}-1\)

\(\Rightarrow S=\frac{(a+1)^{n+1}-1}{n+1}\)