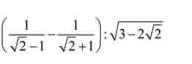Question

Answer 1

\(=\dfrac{\sqrt{2}+1-\sqrt{2}+1}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}\cdot\dfrac{1}{\sqrt{\left(\sqrt{2}-1\right)^2}}\\ =\dfrac{2}{\sqrt{2}-1}=2\sqrt{2}-2\)

Answer 2

\(=\dfrac{\sqrt{2}+1-\sqrt{2}+1}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}\cdot\dfrac{1}{\sqrt{\left(\sqrt{2}-1\right)^2}}\\ =\dfrac{2}{\sqrt{2}-1}=2\sqrt{2}+2\)

Answer 3

\(=\left(\dfrac{\sqrt{2}+1}{2-1}-\dfrac{\sqrt{2}-1}{2-1}\right):\sqrt{\left(\sqrt{2}-1\right)^2}=\left(\sqrt{2}+1-\sqrt{2}+1\right):\left(\sqrt{2}-1\right)=\dfrac{2}{\sqrt{2}-1}=\dfrac{2\left(\sqrt{2}+1\right)}{2-1}=2\left(\sqrt{2}+1\right)\)