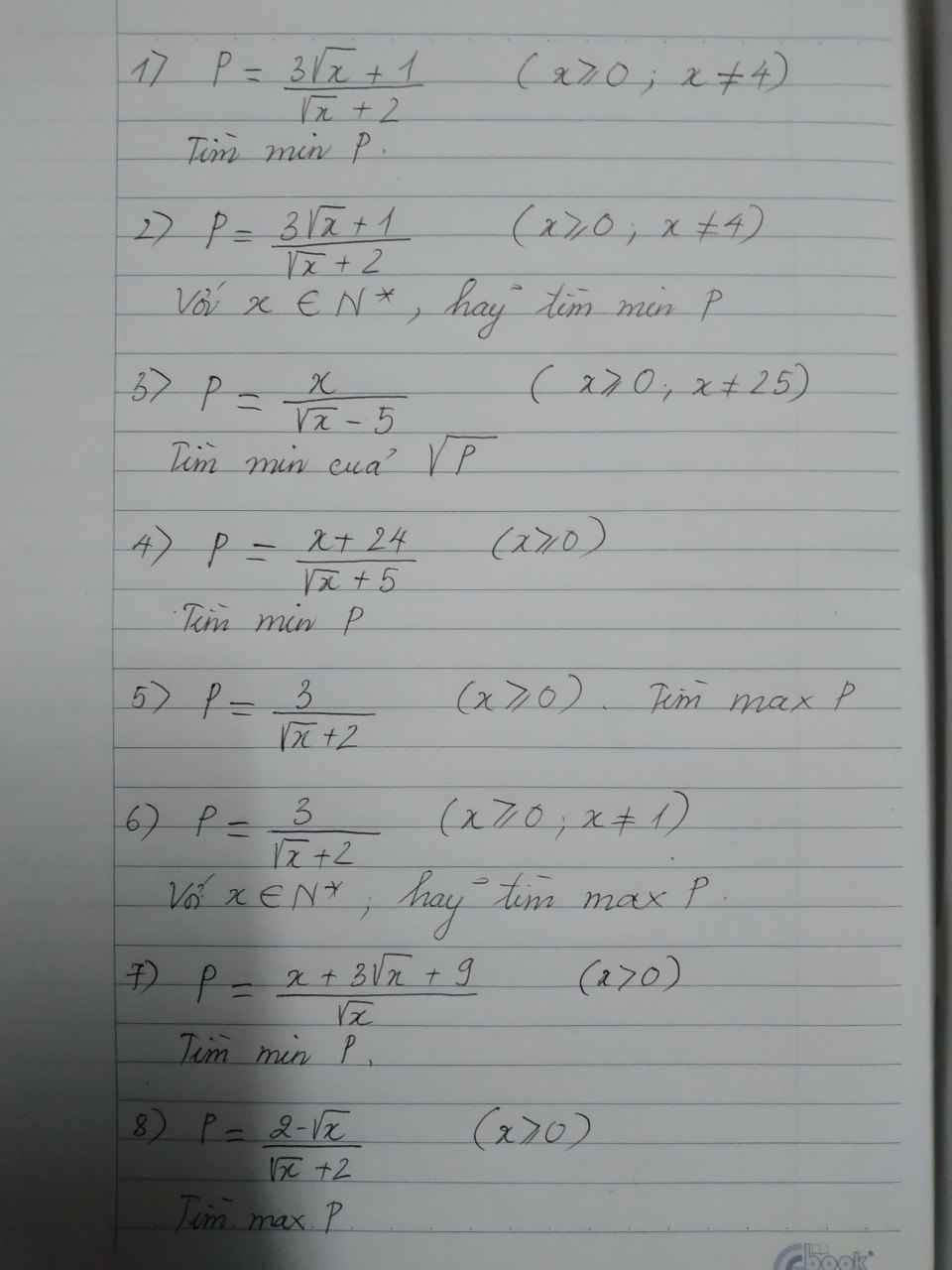Bài 1:
$P=\frac{3(\sqrt{x}+2)-5}{\sqrt{x}+2}$
$=3-\frac{5}{\sqrt{x}+2}$
Ta thấy với $\sqrt{x}\geq 0$ với mọi $x\geq 0$
$\Rightarrow \sqrt{x}+2\geq 2$
$\Rightarrow \frac{5}{\sqrt{x}+2}\leq \frac{5}{2}$
$\Rightarrow P=3-\frac{5}{\sqrt{x}+2}\geq 3-\frac{5}{2}=\frac{1}{2}$
Vậy $P_{\min}=\frac{1}{2}$ khi $x=0$
2.
$P=3-\frac{5}{\sqrt{x}+2}$ (như bài 1)
Ta thấy với mọi $x\in\mathbb{N}^*$ thì $\sqrt{x}\geq 1$
$\Rightarrow \sqrt{x}+2\geq 3$
$\Rightarrow \frac{5}{\sqrt{x}+2}\leq \frac{5}{3}$
$\Rightarrow P=3-\frac{5}{\sqrt{x}+2}\geq 3-\frac{5}{3}=\frac{4}{3}$
Vậy $P_{\min}=\frac{4}{3}$ khi $x=1$
3.
Để $\sqrt{P}$ tồn tại thì $x>25$
Ta có:
\(P=\frac{x}{\sqrt{x}-5}=\frac{x-25+25}{\sqrt{x}-5}=\frac{(\sqrt{x}-5)(\sqrt{x}+5)+25}{\sqrt{x}-5}\)
\(=\sqrt{x}+5+\frac{25}{\sqrt{x}-5}=(\sqrt{x}-5)+\frac{25}{\sqrt{x}-5}+10\)
\(\geq 2\sqrt{25}+10=20\) (theo BĐT AM-GM)
$\Rightarrow \sqrt{P}\geq \sqrt{20}$
Vậy $\sqrt{P}_{\min}=\sqrt{20}$ khi $x=100$
4.
Áp dụng BĐT AM-GM cho các số không âm:
$x+4\geq 4\sqrt{x}$
$\Rightarrow x+24\ge 4\sqrt{x}+20=4(\sqrt{x}+5)$
$\Rightarrow P=\frac{x+24}{\sqrt{x}+5}\ge \frac{4(\sqrt{x}+5)}{\sqrt{x}+5}=4$
Vậy $P_{\min}=4$ khi $x=4$
5.
$\sqrt{x}\geq 0$ với mọi $x\geq 0$
$\Rightarrow \sqrt{x}+2\geq 2$
$\Rightarrow P=\frac{3}{\sqrt{x}+2}\leq \frac{3}{2}$
Vậy $P_{\max}=\frac{3}{2}$
Giá trị này đạt tại $x=0$
6.
Với mọi $x\in\mathbb{N}^*, x\neq 1$ thì $\sqrt{x}\geq \sqrt{2}$
$\Rightarrow \sqrt{x}+2\geq 2+\sqrt{2}$
$\Rightarrow P=\frac{3}{\sqrt{x}+2}\leq \frac{3}{2+\sqrt{2}}$
Vậy $P_{\max}=\frac{3}{2+\sqrt{2}}$ khi $x=2$
7.
\(P=\frac{x+3\sqrt{x}+9}{\sqrt{x}}=\sqrt{x}+3+\frac{9}{\sqrt{x}}=(\sqrt{x}+\frac{9}{\sqrt{x}})+3\)
\(\geq 2\sqrt{9}+3=9\) (áp dụng BĐT AM-GM cho $\sqrt{x}$ và $\frac{9}{\sqrt{x}}$)
Vậy $P_{\min}=9$ khi $x=9$
8.
$\sqrt{x}\geq 0$ với mọi $x\geq 0$
$\Rightarrow \sqrt{x}+2\geq 2$
$\Rightarrow P\leq \frac{2-\sqrt{x}}{2}$
Mà:
$\sqrt{x}\ge 0\Rightarrow 2-\sqrt{x}\leq 2$
$\Rightarrow P\le \frac{2}{2}=1$
Vậy $P_{\max}=1$ khi $x=0$