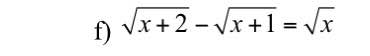Đk:\(x\ge0\)
\(\sqrt{x+2}-\sqrt{x+1}=\sqrt{x}\)
\(\Leftrightarrow\sqrt{x+2}=\sqrt{x}+\sqrt{x+1}\)
\(\Leftrightarrow x+2=2x+1+2\sqrt{x^2+x}\)
\(\Leftrightarrow1-x=2\sqrt{x^2+x}\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-x\ge0\\\left(1-x\right)^2=4\left(x^2+x\right)\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\le1\\3x^2+6x-1=0\end{matrix}\right.\)\(\Rightarrow x=\dfrac{-3\pm2\sqrt{3}}{3}\)
mà \(x\ge0\Rightarrow x=\dfrac{-3+2\sqrt{3}}{3}\)
Vậy...
Đúng 2
Bình luận (0)
