Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{4}x^2-x-m=0\)
\(\text{Δ}=\left(-1\right)^2-4\cdot\dfrac{1}{4}\cdot\left(-m\right)=m+1\)
Vì (P) cắt (d) tại đúng một điểm nên m+1=0
hay m=-1
=>\(\dfrac{1}{4}x^2-x+1=0\)
=>x=2
=>y=1
hàm số y=(-2+m)x+3m đồng biến khi nào
xác đinh tính chẵn - lẻ của các hàm số sau:
a) \(f\left(x\right)=x\left|x\right|\)
b) \(\dfrac{\sqrt{1-x^2}}{x^3+x}\)
tìm hàm xác định
a) f(x)=\(\dfrac{\sqrt{2x+4}}{2x-5}\)
Mọi người giúp em với. E ko bt làm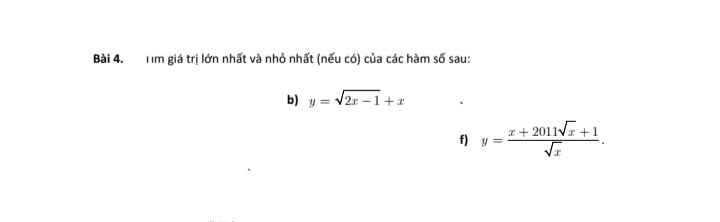
Trong mặt phẳng tọa độ Oxy, cho hàm số y=|x| có đồ thị là (G). Trên đồ thị (G) lấy 2 điểm A,B có hoành độ lần lượt là -1;3
a) Vẽ đồ thị (G) và viết pt đường thẳng (d) đi qua hai điểm A,B
b) Tính khoảng cách từ gốc tọa độ O đến (d)
Tìm các giá trị của tham số m để hàm số: y=x^3+mx đồng biến với mọi x thuộc R.
Cho họ đường thẳng (dm): \(y=\dfrac{m+1}{m^2+m+1}x+\dfrac{m^2}{m^2+m+1}\). Tìm các điểm trên mặt phẳng tọa độ sao cho không có bất kì đường thẳng nào thuộc họ (dm) đi qua.
...
