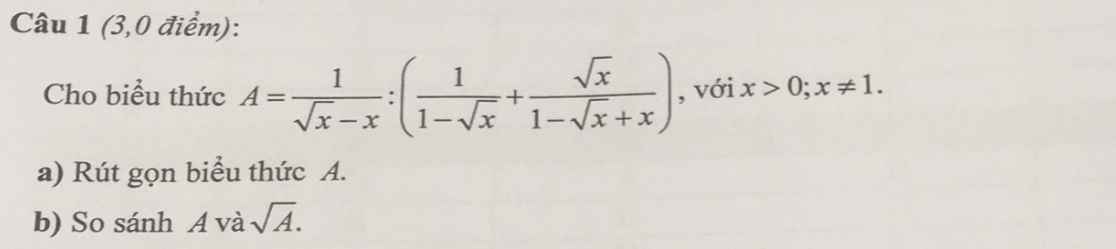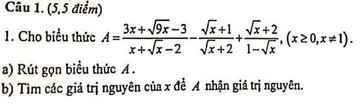So sánh \(\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\) và \(\sqrt{3}\)
Bình phương 2 vế:
VP=3
VT= \(8-2\sqrt{\left(4+\sqrt{7}\right)\left(4-\sqrt{7}\right)}=8-2\sqrt{16-7}=8-6=2\) < VP
Vậy \(\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\) < \(\sqrt{3}\)
Ta có: \(\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\)
\(=\dfrac{\sqrt{7}+1-\sqrt{7}+1}{\sqrt{2}}\)
\(=\sqrt{2}< \sqrt{3}\)