Học tại trường
Chưa có thông tin
Đến từ
Chưa có thông tin , Chưa có thông tin
Số lượng câu hỏi
407
Số lượng câu trả lời
75
Điểm GP
11
Điểm SP
33
Người theo dõi (67)
Đang theo dõi (0)

Chủ đề:
Bài 3. Mô hình xác suất trong một số trò chơi và thí nghiệm đơn giảnCâu hỏi:
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi hai số khác nhau.
Rút ngẫu nhiên một chiếc thẻ trong hộp.
a) Nếu những kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
b) Số xuất hiện trên thẻ được rút ra có phải là phần tử của tập hợp {1; 2; 3; 4; 5} hay không?
c) Viết tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
d) Nêu hai điều cần chú ý trong mô hình xác suất của trò chơi trên.

Chủ đề:
Bài 2. Biểu đồ cột képCâu hỏi:
Biểu đồ ở hình 16 thống kê số lượng ti vi bán được của ba cửa hàng trong tháng 5 và tháng 6 của năm 2018.

a) So sánh số lượng ti vi bán được của mỗi cửa hàng trong tháng 5 và trong tháng 6.
b) Cửa hàng 3 bán được nhiều ti vi nhất trong tháng 5 và tháng 6. Em có thể đưa ra một lí do phù hợp nhất để giải thích cho kết quả này được không? Em đồng ý với những nhận xét nào sau đây:
+) Cửa hàng 3 bán ti vi với giá rẻ nhất ;
+) Cửa hàng 3 chăm sóc khách hàng tốt nhất;
+) Cửa hàng 3 có nhiều loại ti vi cho người mua hàng lựa chọn;
+) Cửa hàng 3 ở vị trí thuận lợi cho việc đi lại mua bán của người mua hàng?
c) Số lượng ti vi mà cả ba cửa hàng bán được trong tháng 6 nhiều hơn số lượng ti vi mà cả ba cửa hàng bán được trong tháng 5 là bao nhiêu chiếc? Em có biết giải bóng đá World Cup 2018 diễn ra vào tháng nào không? Sự kiện đó có liên quan đến việc mua bán ti vi trong tháng 6 hay không?
d) Nếu 20 năm sau (tính từ năm 2018) em có một cửa hàng bán ti vi thì em chọn thời gian nào để có thể bán được nhiều ti vi nhất trong năm?

Chủ đề:
Ôn thi vào 10Câu hỏi:

Câu 1.
Cho biểu thức \(M=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\), \(N=\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\) với \(x\ge0,x\ne4,x\ne9.\)
1) Tính giá trị của biểu thức N khi x = 16,
2) Rút gọn biểu thức M.
3) Tìm tất cả các số tự nhiên x để M < N.
Câu 2.
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Hai người đi xe đạp xuất phát cùng một lúc đi từ A đến B. Vận tốc của họ hơn kém nhau 4 km/h nên đến B sớm muộn hơn nhau 45 phút. Tính vận tốc của mỗi người, biết quãng đường AB dài 36 km.
Câu 3.
1) Giải hệ phương trình: \(\left\{{}\begin{matrix}\dfrac{x+1}{x}+\dfrac{2y+1}{y}=5\\\dfrac{3x+2}{x}+\dfrac{3y+1}{y}=9\end{matrix}\right.\)
2) Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: y = x + m và parabol (P): y = x2.
a) Tìm các tọa độ giao điểm của d và (P) khi m = 6.
b) Tìm m sao cho d cắt (P) tại hai điểm phân biệt có hoành độ dương.
Câu 4.
Cho tam giác ABC vuông tại A và AB < AC. Gọi H là hình chiếu vuông góc của A trên BC và M là điểm đối xứng của H qua AB.
1) Chứng minh tứ giác AMBH nội tiếp.
2) P là giao điểm thứ hai của đường thẳng CM với đường tròn ngoại tiếp tứ giác AMBH. Chứng minh CP.CM = CA2.
3) Gọi E, N lần lượt là giao điểm thứ hai của AB, HP với đường tròn ngoại tiếp tam giác APC. Chứng minh rằng EN song song với BC.
Câu 5.
Giải phương trình: \(\sqrt{x-3}+x^2-6x+7=0\)


Chủ đề:
Bài 1. Thu thập, tổ chức, biểu diễn, phân tích và xử lí số liệuCâu hỏi:
Biểu đồ ở Hình 7 cho biết lượng xuất khẩu của một số mặt hàng chủ yếu ở Việt Nam năm 2018.
.png)
a) Tính theo tấn tổng lượng xuất khẩu của năm mặt hàng trên.
b) Lượng gạo xuất khẩu nhiều hơn tổng lượng xuất khẩu của bốn mặt hàng còn lại là bao nhiêu tấn?

Chủ đề:
Bài 1. Thu thập, tổ chức, biểu diễn, phân tích và xử lí số liệuCâu hỏi:
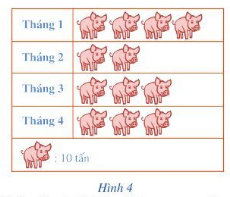
Một hệ thống siêu thị thống kê lượng thịt lợn bán được trong bốn tháng đầu năm 2020 ở biểu đồ trong Hình 4. a) Tháng nào hệ thống siêu thị bán được nhiều thịt lợn nhất? b) Tính tỉ số của lượng thịt lớn bán ra trong tháng 1 và tổng lượng thịt lợn bán ra trong cả bốn tháng. |
|

Chủ đề:
Bài 1. Thu thập, tổ chức, biểu diễn, phân tích và xử lí số liệuCâu hỏi:
Bác Hoàn khai trương cửa hàng bán áo sơ mi. Thống kê số lượng các loại áo đã bán bán trong tháng đầu tiên như bảng sau (đơn vị tính: chiếc):
| Cỡ áo | 37 | 38 | 39 | 40 | 41 | 42 |
| Số áo bán được | 20 | 29 | 56 | 65 | 47 | 18 |
a) Áo cỡ nào bán được nhiều nhất? Ít nhất?
b) Bác Hoàn nên nhập về nhiều hơn những loại áo cỡ nào để bán trong tháng tiếp theo?