Bài 39 trang 124 Trên mỗi hình 105,106,108 các tam giác vuông nào bằng nhau? Vì sao?

Hình 105. ∆ABHvà ∆ACH có:
BH=CH(gt)
∠AHB = ∠AHC (∠vuông)
AH là cạnh chung.
vậy ∆ABH=∆ACH(c.g.c)
Hình 106. ∆DKE và ∆DKF có:
∠EDK = ∠FDK(gt)
DK là cạnh chung.
∠DKE = ∠DKF(∠vuông)
Vậy ∆DKE=∆DKF(g.c.g)
Hình 107. Ta có:
∠BAD = ∠CAD (gt)
AD chung
∆ABD=∆ACD(Cạnh huyền∠nhọn).
Hình 108. Δ ABD = Δ ACD (Cạnh huyền ∠nhọn)
⇒ AB = AC, DB = DC
Δ DBE = Δ DCH (g.c.g)
∆ABH=ACE (g.c.g)
40. Cho ΔABC(AB≠AC), tia Ax đi qua trung điểm M của BC.
Kẻ BE và CF ⊥ với Ax(E ∈ Ax, F∈Ax ). So sánh độ dài BE và CF/
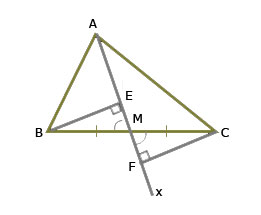
Hai Δ vuông BME, CMF có:
BM=MC(gt)
∠BME = ∠CMF(đối đỉnh)
Nên ∆BME=∆CMF(cạnh huyền- ∠nhọn).
Suy ra BE=CF. (2 cạnh tương ứng).
41. Cho ΔABC, cac tia phân giác của các ∠B và C cắt nhau ở I. Vẽ ID ⊥AB(D nằm trên AB), IE ⊥ BC (E thuộc BC ), IF ⊥ với AC(F thuộc AC)
CMR: ID=IE=IF.
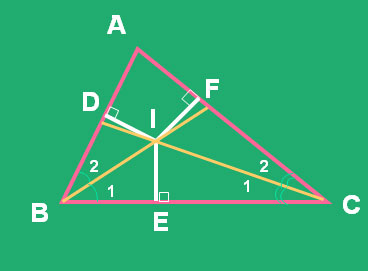
Hai Δvuông BID và BIE có:
BI là cạnh chung
∠B1 = ∠B2(do BI là tia phân giác ∠B)
nên ∆BID=∆BIE. (cạnh huyền – ∠nhọn)
Suy ra ID=IE (2 cạnh tương ứng) (1)
Tương tự:
CI là cạnh chung
∠C1 = ∠C2(do CI là tia phân giác ∠C)
∆CIE=CIF(cạnh huyền ∠nhọn).
Suy ra: IE =IF (2 cạnh tương ứng) (2)
Từ (1)(2) suy ra: ID=IE=IF.
42. Cho ΔABC có ∠A= 900, kẻ AH ⊥ BC(H∈BC). C ác ΔAHC và BAC có AC là cạnh chung, ∠C chung, ∠AHC = ∠BAC =900, nhưng hai Δkhông bằng nhau. Tại sao ở đây không áp dụng trường hợp góc cạnh góc để kết luận ∆AHC= ∆BAC?

ΔAHC và BAC có:
AC là cạnh chung
∠C chung.
∠AHC = ∠BAC=900, Nhưng hai tam giác không bằng nhau vì ∠AHC không phải là ∠kề với AC.

















