Câu trả lời:
c) (O) tiếp xúc với AC tại H.
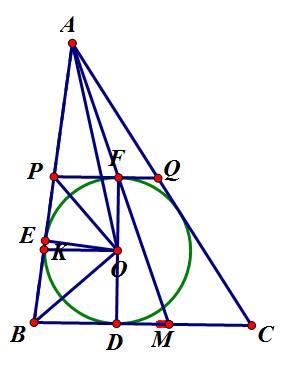
△ABC có (O) tiếp xúc với BC,AB,CA lần lượt tại D,E,H.
\(\Rightarrow BD=BE;AE=AH;CD=CH\)
\(BD+BE=AB-AE+BC-CD=AB+BC-AH-CH=AB+BC-AC\)
\(\Rightarrow BD=\dfrac{AB+BC-CA}{2}\left(3\right)\)
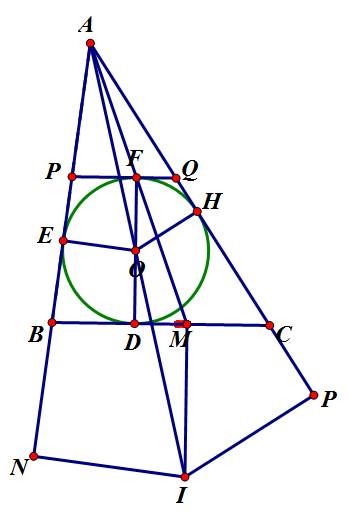
*Qua M kẻ đường thẳng vuông góc với BC cắt tia AO tại I.
*Hạ IN⊥AB tại N, IP⊥CA tại P.
Xét △AIM có: OF//IM \(\Rightarrow\dfrac{OF}{IM}=\dfrac{AO}{AI}\) (4) (hệ quả định lí Thales)
Xét △AIN có: OE//IN \(\Rightarrow\dfrac{OE}{IN}=\dfrac{AO}{AI}\) (5) (hệ quả định lí Thales)
Ta cũng có \(OE=OF\left(6\right)\) (bằng bán kính của (O) )
\(\left(4\right),\left(5\right),\left(6\right)\Rightarrow IM=IN\)
Dễ dàng chứng minh △BNI=△BMI (ch-cgv) nên \(\widehat{NBI}=\widehat{MBI}\)
\(\Rightarrow BI\) là phân giác của góc NBC hay BI là phân giác ngoài của △ABC.
Xét △ABC có: Phân giác trong góc A (AO) cắt phân giác ngoài góc B (BI) tại I.
\(\Rightarrow\)I là tâm đường tròn bàng tiếp ở đỉnh A.
Lại có IN⊥AB tại N, IM⊥BC tại M, IP⊥AC tại P.
\(\Rightarrow\)IN,IP,IM là các bán kính của (I).
\(\Rightarrow\)(I) tiếp xúc với AB,BC,CA lần lượt tại N,M,P.
\(\Rightarrow AN=AP;BN=BM;CM=CP\)
\(CM+CP=BC-BM+AP-AC=BC-AC+AN-BN=BC-AC+AB\)
\(\Rightarrow CM=\dfrac{BC+AB-AC}{2}\left(7\right)\)
\(\left(3\right),\left(7\right)\Rightarrow BD=CM\)