Bài 3: Phương trình quy về phương trình bậc hai
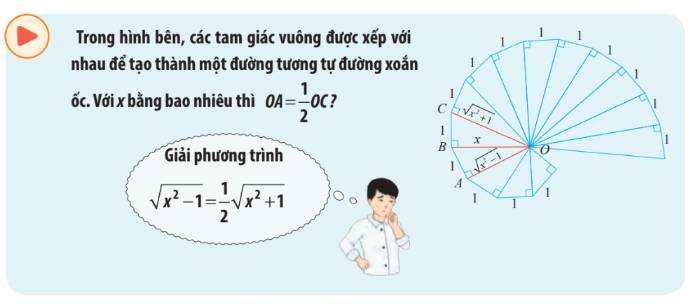
Khởi động (SGK Chân trời sáng tạo trang 15,16)
Thảo luận (1)
Khám phá 1 (SGK Chân trời sáng tạo trang 15,16)
Lời giải cho phương trình sqrt { - 2{x^2} - 2x + 11} sqrt { - {x^2} + 3} như sau đúng hai sai?sqrt { - 2{x^2} - 2x + 11} sqrt { - {x^2} + 3} Rightarrow - 2{x^2} - 2x + 11 - {x^2} + 3 (bình phương cả hai vế để làm mất dấu căn) Rightarrow {x^2} + 2x - 8 0 (chuyển vế, rút gọn) Rightarrow x 2 hoặc x - 4 (giải phương trình bậc hai)Vậy phương trình đã cho có hai nghiệm là 2 và -4.
Đọc tiếp
Lời giải cho phương trình \(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \) như sau đúng hai sai?
\(\)\(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \)
\( \Rightarrow - 2{x^2} - 2x + 11 = - {x^2} + 3\) (bình phương cả hai vế để làm mất dấu căn)
\( \Rightarrow {x^2} + 2x - 8 = 0\) (chuyển vế, rút gọn)
\( \Rightarrow x = 2\) hoặc \(x = - 4\) (giải phương trình bậc hai)
Vậy phương trình đã cho có hai nghiệm là 2 và -4.
Thảo luận (1)Hướng dẫn giảiThay \(x = 2\) vào phương trình \(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \) ta thấy không thỏa mãn vì dưới dấu căn là \( - 1\) không thỏa mãn
Vậy \(x = 2\) không là nghiệm của phương trình do đó lời giải như trên là sai.
(Trả lời bởi Hà Quang Minh)
Thực hành 1 (SGK Chân trời sáng tạo trang 15,16)
Giải phương trình \(\sqrt {31{x^2} - 58x + 1} = \sqrt {10{x^2} - 11x - 19} \).
Thảo luận (1)Hướng dẫn giảiBình phương hai vế của phương trình đã cho, ta được:
\(\begin{array}{l}\sqrt {31{x^2} - 58x + 1} = \sqrt {10{x^2} - 11x - 19} \\ \Rightarrow 31{x^2} - 58x + 1 = 10{x^2} - 11x - 19\\ \Rightarrow 21{x^2} - 47x + 20 = 0\end{array}\)
\( \Rightarrow x = \frac{5}{3}\) hoặc \(x = \frac{4}{7}\)
Thay lần lượt các nghiệm trên vào phương trình đã cho, ta thấy không có nghiệm nào thỏa mãn
Vậy phương trình đã cho vô nghiệm
Chú ý khi giải: sau khi bình phương hai vế thì các bước giải tiếp theo chỉ được sử dụng dấu suy ra không được sử dụng dấu tương đương (vì tập nghiệm của chúng có thể không giống nhau)
(Trả lời bởi Hà Quang Minh)
Khám phá 2 (SGK Chân trời sáng tạo trang 16,17)
Lời giải cho phương trình sqrt { - {x^2} + x + 1} x như sau đúng hai sai?sqrt { - {x^2} + x + 1} x Rightarrow - {x^2} + x + 1 {x^2} (bình phương cả hai vế để làm mất dấu căn) Rightarrow - 2{x^2} + x + 1 0 (chuyển vế, rút gọn) Rightarrow x 1 hoặc x - frac{1}{2} (giải phương trình bậc hai)Vậy phương trình đã cho có hai nghiệm là 1 và - frac{1}{2}
Đọc tiếp
Lời giải cho phương trình \(\sqrt { - {x^2} + x + 1} = x\) như sau đúng hai sai?
\(\)\(\sqrt { - {x^2} + x + 1} = x\)
\( \Rightarrow - {x^2} + x + 1 = {x^2}\) (bình phương cả hai vế để làm mất dấu căn)
\( \Rightarrow - 2{x^2} + x + 1 = 0\) (chuyển vế, rút gọn)
\( \Rightarrow x = 1\) hoặc \(x = - \frac{1}{2}\) (giải phương trình bậc hai)
Vậy phương trình đã cho có hai nghiệm là 1 và \( - \frac{1}{2}\)
Thảo luận (1)Hướng dẫn giảiThay nghiệm tìm được vào phương trình ban đầu ta có:
+) Thay \(x = 1\) vào phương trình \(\sqrt { - {x^2} + x + 1} = x\) ta thấy thảo mãn phương trình
+) Thay \(x = - \frac{1}{2}\) vào \(\sqrt { - {x^2} + x + 1} = x\) ta thấy không thỏa mãn phương trình
Vậy nghiệm của phương trình là \(x = 1\), suy ra lời giải như trên là sai.
(Trả lời bởi Hà Quang Minh)
Thực hành 2 (SGK Chân trời sáng tạo trang 16,17)
Giải phương trình \(\sqrt {3{x^2} + 27x - 41} = 2x + 3\)
Thảo luận (1)Hướng dẫn giảiBình phương hai vế của phương trình đã cho, ta được:
\(3{x^2} + 27x - 41 = {\left( {2x + 3} \right)^2}\)
\( \Rightarrow 3{x^2} + 27x - 41 = 4{x^2} + 12x + 9\)
\( \Rightarrow {x^2} - 15x + 50 = 0\)
\( \Rightarrow x = 5\) và \(x = 10\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {3{x^2} + 27x - 41} = 2x + 3\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy nghiệm của phương trình đã cho là \(x = 5\) và \(x = 10\)
(Trả lời bởi Hà Quang Minh)
Vận dụng (SGK Chân trời sáng tạo trang 16,17)
Cho tam giác OAB và OBC lần lượt vuông tại A và B như hình 1. Các cạnh AB và BC bằng nhau và ngắn hơn OB là 1 cm. Hãy biểu diễn độ dài OC và OA qua OB, từ đó xác định OB để:
a) \(OC = 3OA;\)
b) \(OC = \frac{5}{4}OB\)
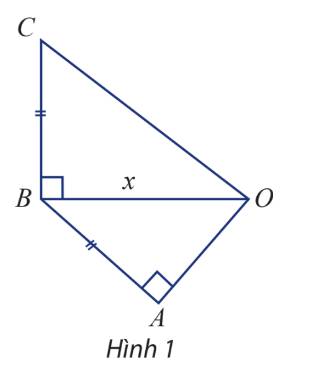
Thảo luận (1)Hướng dẫn giảiGọi độ dài cạnh OB là x cm \(\left( {x > 0} \right)\)
Theo giả thiết ta có \(AB = BC = OB - 1 = x - 1\)
Áp dụng định lý pitago trong tam giác vuông OAB và OBC ta có:
\(OC = \sqrt {O{B^2} + B{C^2}} = \sqrt {{x^2} + {{\left( {x - 1} \right)}^2}} = \sqrt {2{x^2} - 2x + 1} \)
\(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{x^2} - {{\left( {x - 1} \right)}^2}} = \sqrt {2x - 1} \)
a) \(OC = 3OA \Rightarrow \sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = 9\left( {2x - 1} \right)\\ \Rightarrow 2{x^2} - 20x + 10 = 0\end{array}\)
\( \Rightarrow \)\(x = 5 - 2\sqrt 5 \) và \(x = 5 + 2\sqrt 5 \)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \) ta thấy cả hai đều thỏa mãn phương trình
Vậy khi \(OB = 5 - 2\sqrt 5 \) hoặc \(OB = 5 + 2\sqrt 5 \)thì \(OC = 3OA\)
b) \(OC = \frac{5}{4}OB \Rightarrow \sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = \frac{{25}}{{16}}{x^2}\\ \Rightarrow \frac{7}{{16}}{x^2} - 2x + 1 = 0\end{array}\)\(\)
\( \Rightarrow x = \frac{4}{7}\) hoặc \(x = 4\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(OB = \frac{4}{7}\) hoặc \(OB = 4\) (cm) thì \(OC = \frac{5}{4}OB\)
(Trả lời bởi Hà Quang Minh)
Bài 1 (SGK Chân trời sáng tạo trang 17)
Giải các phương trình sau:
a) \(\sqrt {11{x^2} - 14x - 12} = \sqrt {3{x^2} + 4x - 7} \)
b) \(\sqrt {{x^2} + x - 42} = \sqrt {2x - 30} \)
c) \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \)
d) \(3\sqrt {{x^2} + x - 1} - \sqrt {7{x^2} + 2x - 5} = 0\)
Thảo luận (1)Hướng dẫn giảia) \(\sqrt {11{x^2} - 14x - 12} = \sqrt {3{x^2} + 4x - 7} \)
\(\begin{array}{l} \Rightarrow 11{x^2} - 14x - 12 = 3{x^2} + 4x - 7\\ \Rightarrow 8{x^2} - 18x - 5 = 0\end{array}\)
\( \Rightarrow x = - \frac{1}{4}\) và \(x = \frac{5}{2}\)
Thay nghiệm vừa tìm được vào phương trình \(\sqrt {11{x^2} - 14x - 12} = \sqrt {3{x^2} + 4x - 7} \) ta thấy chỉ có nghiệm \(x = \frac{5}{2}\) thảo mãn phương trình
Vậy nhiệm của phương trình đã cho là \(x = \frac{5}{2}\)
b) \(\sqrt {{x^2} + x - 42} = \sqrt {2x - 30} \)
\(\begin{array}{l} \Rightarrow {x^2} + x - 42 = 2x - 3\\ \Rightarrow {x^2} - x - 12 = 0\end{array}\)
\( \Rightarrow x = - 3\) và \(x = 4\)
Thay vào phương trình \(\sqrt {{x^2} + x - 42} = \sqrt {2x - 30} \) ta thấy không có nghiệm nào thỏa mãn
Vậy phương trình đã cho vô nghiệm
c) \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \)
\(\begin{array}{l} \Rightarrow 4.\left( {{x^2} - x - 1} \right) = {x^2} + 2x + 5\\ \Rightarrow 3{x^2} - 6x - 9 = 0\end{array}\)
\( \Rightarrow x = - 1\) và \(x = 3\)
Thay hai nghiệm trên vào phương trình \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \) ta thấy cả hai nghiệm đếu thỏa mãn phương trình
Vậy nghiệm của phương trình \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \) là \(x = - 1\) và \(x = 3\)
d) \(3\sqrt {{x^2} + x - 1} - \sqrt {7{x^2} + 2x - 5} = 0\)
\(\begin{array}{l} \Rightarrow 3\sqrt {{x^2} + x - 1} = \sqrt {7{x^2} + 2x - 5} \\ \Rightarrow 9.\left( {{x^2} + x - 1} \right) = 7{x^2} + 2x - 5\\ \Rightarrow 2{x^2} + 7x - 4 = 0\end{array}\)
\( \Rightarrow x = - 4\) và \(x = \frac{1}{2}\)
Thay hai nghiệm trên vào phương trình \(3\sqrt {{x^2} + x - 1} - \sqrt {7{x^2} + 2x - 5} = 0\) ta thấy chỉ có nghiệm \(x = - 4\) thỏa mãn phương trình
Vậy nghiệm của phương trình trên là \(x = - 4\)
(Trả lời bởi Hà Quang Minh)
Bài 2 (SGK Chân trời sáng tạo trang 17)
Giải các phương trình sau:
a) \(\sqrt {{x^2} + 3x + 1} = 3\)
b) \(\sqrt {{x^2} - x - 4} = x + 2\)
c) \(2 + \sqrt {12 - 2x} = x\)
d) \(\sqrt {2{x^2} - 3x - 10} = - 5\)
Thảo luận (1)Hướng dẫn giảia) \(\sqrt {{x^2} + 3x + 1} = 3\)
\(\begin{array}{l} \Rightarrow {x^2} + 3x + 1 = 9\\ \Rightarrow {x^2} + 3x - 8 = 0\end{array}\)
\( \Rightarrow x = \frac{{ - 3 - \sqrt {41} }}{2}\) và \(x = \frac{{ - 3 + \sqrt {41} }}{2}\)
Thay hai nghiệm trên vào phương trình \(\sqrt {{x^2} + 3x + 1} = 3\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy nghiệm của phương trình đã cho là \(x = \frac{{ - 3 - \sqrt {41} }}{2}\) và \(x = \frac{{ - 3 + \sqrt {41} }}{2}\)
b) \(\sqrt {{x^2} - x - 4} = x + 2\)
\(\begin{array}{l} \Rightarrow {x^2} - x - 4 = {\left( {x + 2} \right)^2}\\ \Rightarrow {x^2} - x - 4 = {x^2} + 4x + 4\\ \Rightarrow 5x = - 8\\ \Rightarrow x = - \frac{8}{5}\end{array}\)
Thay \(x = - \frac{8}{5}\) và phương trình \(\sqrt {{x^2} - x - 4} = x + 2\) ta thấy thỏa mãn phương trình
Vậy nghiệm của phương trình đã cho là \(x = - \frac{8}{5}\)
c) \(2 + \sqrt {12 - 2x} = x\)
\(\begin{array}{l} \Rightarrow \sqrt {12 - 2x} = x - 2\\ \Rightarrow 12 - 2x = {\left( {x - 2} \right)^2}\\ \Rightarrow 12 - 2x = {x^2} - 4x + 4\\ \Rightarrow {x^2} - 2x - 8 = 0\end{array}\)
\( \Rightarrow x = - 2\) và \(x = 4\)
Thay hai nghiệm vừa tìm được vào phương trình \(2 + \sqrt {12 - 2x} = x\) thì thấy chỉ có \(x = 4\) thỏa mãn
Vậy \(x = 4\) là nghiệm của phương trình đã cho.
d) Ta có biểu thức căn bậc hai luôn không âm nên \(\sqrt {2{x^2} - 3x - 10} \ge 0\forall x \in \mathbb{R}\)
\( \Rightarrow \sqrt {2{x^2} - 3x - 10} = - 5\) (vô lí)
Vậy phương trình đã cho vô nghiệm
(Trả lời bởi Hà Quang Minh)
Bài 3 (SGK Chân trời sáng tạo trang 17)
Cho tam giác ABC vuông tại A có AB ngắn hơn AC là 2 cm.
a) Biểu diễn độ dài cạnh huyền BC theo AB
b) Biết chu vi của tam giác ABC là 24 cm. Tính độ dài ba cạnh của tam giác đó.
Thảo luận (2)Hướng dẫn giải
a) Đặt độ dài cạnh AB là x (\(x > 0\))
Theo giả thiết ta có độ dài \(AC = AB + 2 = x + 2\)
Áp dụng định lý pitago trong tam giác vuông ta có
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{x^2} + {{\left( {x + 2} \right)}^2}} = \sqrt {2{x^2} + 4x + 4} \)
b) Chu vi của tam giác là \(C = AB + AC + BC\)
\( \Rightarrow C = x + \left( {x + 2} \right) + \sqrt {2{x^2} + 4x + 4} = 2x + 2 + \sqrt {2{x^2} + 4x + 4} \)
Theo giả thiết ta có
\(\begin{array}{l}C = 24 \Leftrightarrow 2x + 2 + \sqrt {2{x^2} + 4x + 4} = 24\\ \Leftrightarrow \sqrt {2{x^2} + 4x + 4} = 22 - 2x\\ \Rightarrow 2{x^2} + 4x + 4 = {\left( {22 - 2x} \right)^2}\\ \Rightarrow 2{x^2} + 4x + 4 = 4{x^2} - 88x + 484\\ \Rightarrow 2{x^2} - 92x + 480 = 0\end{array}\)
\( \Rightarrow x = 6\) hoặc \(x = 40\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} + 4x + 4} = 22 - 2x\) ta thấy chỉ có \(x = 6\) thỏa mãn phương trình
Vậy độ dài ba cạnh của tam giác là \(AB = 6;AC = 8\) và \(BC = 10\)(cm)
(Trả lời bởi Hà Quang Minh)
Bài 4 (SGK Chân trời sáng tạo trang 17)
Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc 60^circ . Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng 1km và 2km (Hình 2).a) Đặt độ dài của MO là x km. Biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x.b) Tìm x để khoảng cách từ tàu đến B bằng frac{4}{5} khoảng cách từ tàu đến Ac) Tìm x để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.Lưu ý: Làm tròn kết quả đến hàng phầ...
Đọc tiếp
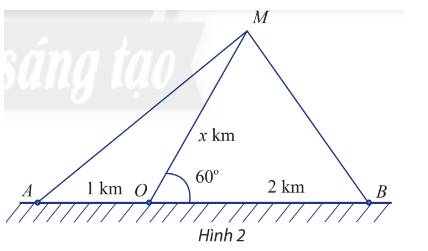
Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc \(60^\circ \). Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng 1km và 2km (Hình 2).
a) Đặt độ dài của MO là x km. Biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x.
b) Tìm x để khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A
c) Tìm x để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.
Lưu ý: Làm tròn kết quả đến hàng phần trăm.
Thảo luận (1)Hướng dẫn giảia) Đặt độ dài của MO là x km \(\left( {x > 0} \right)\)
Ta có: \(\widehat {MOA} + \widehat {MOB} = 180^\circ \) (hai góc bù nhau) \( \Rightarrow \widehat {MOA} = 120^\circ \)
Áp dụng định lý Cosin trong tam giác ta tính được:
+) Khoảng cách từ tàu đến B là \(MB = \sqrt {{x^2} + {2^2} - 2.2.x.\cos 60^\circ } = \sqrt {{x^2} - 2x + 4} \)
+) Khoảng cách từ tàu đến A là \(MA = \sqrt {{x^2} + {1^2} - 2.1.x.\cos 120^\circ } = \sqrt {{x^2} + x + 1} \)
b) Theo giải thiết ta có phương trình \(MB = \frac{4}{5}MA \Rightarrow \sqrt {{x^2} - 2x + 4} = \frac{4}{5}\sqrt {{x^2} + x + 1} \)
\(\begin{array}{l} \Rightarrow {x^2} - 2x + 4 = \frac{{16}}{{25}}\left( {{x^2} + x + 1} \right)\\ \Rightarrow \frac{9}{{25}}{x^2} - \frac{{66}}{{25}}x + \frac{{84}}{{25}} = 0\end{array}\)
\( \Rightarrow x \simeq 1,64\) và \(x \simeq 5,69\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {{x^2} - 2x + 4} = \frac{4}{5}\sqrt {{x^2} + x + 1} \) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(x \simeq 1,64\) hoặc \(x \simeq 5,69\) thì khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A
c) Đổi 500 m = 0,5 km
Theo giả thiết ta có phương trình sau:
\(\begin{array}{l}MB = MO - 0,5 \Rightarrow \sqrt {{x^2} - 2x + 4} = x - 0,5\\ \Rightarrow {x^2} - 2x + 4 = {\left( {x - 0,5} \right)^2}\\ \Rightarrow {x^2} - 2x + 4 = {x^2} - x + \frac{1}{4}\\ \Rightarrow x = \frac{{15}}{4}\end{array}\)
Thay \(x = \frac{{15}}{4}\) vào phương trình \(\sqrt {{x^2} - 2x + 4} = x - 0,5\) ta thấy thỏa mãn phương trình
Vậy khi \(x = \frac{{15}}{4}\) thì khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.
(Trả lời bởi Hà Quang Minh)
