Bài 25. Phép cộng và phép trừ phân số

Hướng dẫn giải

a) \(\dfrac{3}{5} - \dfrac{{ - 1}}{3}\)

\( = \dfrac{{3.3}}{{5.3}} - \dfrac{{ - 1.5}}{{3.5}}\)

\( = \dfrac{9}{{15}} - \dfrac{{ - 5}}{{15}} = \dfrac{{9 - \left( { - 5} \right)}}{{15}} = \dfrac{{14}}{{15}}\)

b) \( - 3 - \dfrac{2}{7}\)

\(\begin{array}{l} = \dfrac{{ - 3.7}}{{1.7}} - \dfrac{2}{7}\\ = \dfrac{{ - 21}}{7} - \dfrac{2}{7}\\ = \dfrac{{ - 21 - 2}}{7}\\ = \dfrac{{ - 23}}{7}\end{array}\)

(Trả lời bởi Hà Quang Minh)

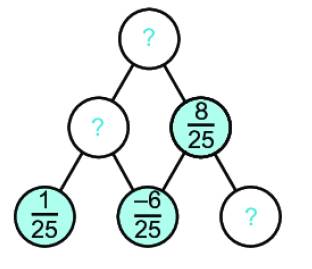
Hướng dẫn giải

Quy luật: số trong ô ở hàng trên = tổng 2 số trong 2 ô dưới nó

Dấu “?b” ở đây bằng \(\dfrac{1}{{25}} + \dfrac{{ - 6}}{{25}} = \dfrac{{1 + \left( { - 6} \right)}}{{25}} = \dfrac{{ - 5}}{{25}} = \dfrac{{ - 1}}{5}\)

Dấu “?c” ở đây bằng \(\dfrac{8}{{25}} - \dfrac{{ - 6}}{{25}} = \dfrac{{8 - \left( { - 6} \right)}}{{25}} = \dfrac{{14}}{{25}}\)

Dấu “?a” ở đây bằng \(\dfrac{8}{{25}} + \dfrac{{ - 5}}{{25}} = \dfrac{3}{{25}}\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

\(\begin{array}{l}\dfrac{1}{2} + \dfrac{{ - 1}}{2} = \dfrac{{1 +(-1)}}{2} = \dfrac{0}{2} = 0\\\dfrac{1}{2} + \dfrac{1}{{ - 2}} = \dfrac{1}{2} + \dfrac{1.(-1)}{{ (- 2).(-1)}} = \dfrac{1}{2} + \dfrac{{ - 1}}{2} =\dfrac{0}{2} = 0\end{array}\)

Các phép tính trên đều có kết quả bằng 0.

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

* Quy tắc trừ hai phân số cùng mẫu: Muốn trừ 2 phân số có cùng mẫu số, ta lấy tử số của phân số thứ nhất trừ đi tử số của phân số thứ hai và giữ nguyên mẫu.

* Ta có: \(\dfrac{7}{{13}} - \dfrac{5}{{13}} = \dfrac{{7 - 5}}{{13}} = \dfrac{2}{{13}}\) và \(\dfrac{3}{4} - \dfrac{1}{5} = \dfrac{{15}}{{20}} - \dfrac{4}{{20}} = \dfrac{{15 - 4}}{{20}} = \dfrac{{11}}{{20}}\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

Số đối của \(\dfrac{1}{3}\)  là \( - \dfrac{1}{3}\) vì \(\dfrac{1}{3} + \left( { - \dfrac{1}{3}} \right) = 0\)

Số đối của \(\dfrac{{ - 1}}{3}\) là \(\dfrac{1}{3}\) vì \(\dfrac{1}{3} + \dfrac{{ - 1}}{3} = \dfrac{1}{3} + \left( { - \dfrac{1}{3}} \right) = 0\)

Số đối của \(\dfrac{{ - 4}}{5}\) là \(\dfrac{4}{5}\) vì \(\dfrac{{ - 4}}{5} + \dfrac{4}{5} = \dfrac{{ - 4 + 4}}{5} = 0\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

BCNN(8,20) = 40

\(\dfrac{{ - 5}}{8}+ \dfrac{{ - 7}}{{20}} = \dfrac{{ - 5.5}}{{8.5}} + \dfrac{{ - 7.2}}{{20.2}} \\=\dfrac{{ - 25}}{{40}}+ \dfrac{{ - 14}}{{40}} = \dfrac{{ - 25 + \left( { - 14} \right)}}{{40}} = \dfrac{{ - 39}}{{40}}\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

\(\dfrac{{ - 7}}{{12}} + \dfrac{5}{{12}} = \dfrac{{ - 7 + 5}}{{12}} = \dfrac{{ - 2}}{{12}} =  \dfrac{{ - 1}}{{6}}\) ;   

\(\dfrac{{ - 8}}{{11}} + \dfrac{{ - 19}}{{11}} = \dfrac{{ - 8 + \left( { - 19} \right)}}{{11}} = \dfrac{{ - 27}}{{11}}\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

Quy tắc cộng hai số nguyên cùng mẫu:

Ta lấy tử số cộng với nhau và giữ nguyên mẫu số.

+) \(\dfrac{8}{{11}} + \dfrac{3}{{11}} = \dfrac{{8 + 3}}{{11}} = \dfrac{{11}}{{11}} = 1\)

+) \(\dfrac{9}{{12}} + \dfrac{{11}}{{12}} = \dfrac{{9 + 11}}{{12}} = \dfrac{{20}}{{12}}\)\( = \dfrac{{20:4}}{{12:4}} = \dfrac{5}{3}\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

Ta có: \(\dfrac{5}{7} = \dfrac{{5.4}}{{7.4}} = \dfrac{{20}}{{28}}\) và \(\dfrac{{ - 3}}{4} = \dfrac{{ - 3.7}}{{4.7}} = \dfrac{{ - 21}}{{28}}\)

Như vậy, \(\dfrac{{20}}{{28}} + \dfrac{{ - 21}}{{28}} = \dfrac{{20 + \left( { - 21} \right)}}{{28}} =  \dfrac{-1}{{28}}\)

(Trả lời bởi Hà Quang Minh)

Hướng dẫn giải

\(\begin{array}{l}B = \dfrac{{ - 1}}{9} + \dfrac{8}{7} + \dfrac{{10}}{9} + \dfrac{{ - 29}}{7}\\ = \left( {\dfrac{{ - 1}}{9} + \dfrac{{10}}{9}} \right) + \left( {\dfrac{8}{7} + \dfrac{{ - 29}}{7}} \right)\\ = \dfrac{9}{9} + \dfrac{{ - 21}}{7} = 1 - 3 =  - 2\end{array}\)

(Trả lời bởi Hà Quang Minh)