Hai quả cầu tích điện cùng dấu được treo bằng hai sợi dây mảnh không dẫn điện như hình bên. Tại sao chúng không tiếp xúc nhưng vẫn tương tác được với nhau?
Hai quả cầu tích điện cùng dấu được treo bằng hai sợi dây mảnh không dẫn điện như hình bên. Tại sao chúng không tiếp xúc nhưng vẫn tương tác được với nhau?

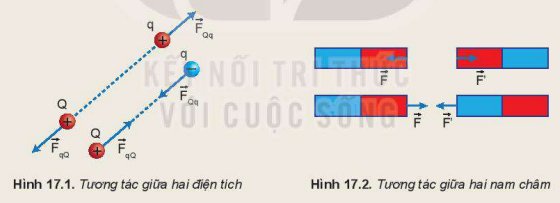
Đặt điện tích q cách điện tích Q một khoảng r (Hình 17.1):
1. Có phải không khí đã truyền tương tác điện từ điện tích Q tới điện tích q?
2. Vùng không gian bao quanh một nam châm có từ trường. Tương tự như vậy, vùng không gian bao quanh một điện tích có điện trường. Ta có thể phát hiện sự tồn tại của điện trường bằng cách nào?
Thảo luận (1)Hướng dẫn giảiTham khảo:
1. Không phải không khí đã truyền tương tác điện từ điện tích Q tới điện tích q. Mà do xung quanh điện tích Q có điện trường, khi điện tích q đặt trong điện trường đó sẽ chịu lực điện do điện trường của Q gây ra.
2. Để phát hiện điện trường ta dùng điện tích thử, đặt vào trong vùng nghi có điện trường, nếu có sự tương tác chứng tỏ xung quanh đó có điện trường.
(Trả lời bởi HT.Phong (9A5))
Hãy chứng tỏ rằng vectơ cường độ điện trường \(\overrightarrow{E}\) có:
+ Phương trùng với phương của lực điện tác dụng lên điện tích.
+ Chiều cùng với chiều của lực điện khi q > 0, ngược chiều với chiều của lực điện khi q < 0.
+ Độ lớn của vectơ cường độ điện trường \(\overrightarrow{E}\) bằng độ lớn của lực điện tác dụng lên điện tích 1C đặt tại điểm ta xét.
Thảo luận (1)Hướng dẫn giảiTa có: \(\overrightarrow E = \frac{{\overrightarrow F }}{q}\)
Từ công thức ta thấy vectơ cường độ điện trường \(\overrightarrow E \) có phương trùng với phương của lực điện tác dụng lên điện tích
Với q > 0 thì \(\overrightarrow E \),\(\overrightarrow F \) cùng chiều với nhau
Với q < 0 thì \(\overrightarrow E \),\(\overrightarrow F \)ngược chiều với nhau
Nếu q = 1 thì E = F
(Trả lời bởi Hà Quang Minh)
Xét điện trường của điện tích Q = 6.10-14 C, sử dụng đoạn thẳng dài 1 cm để biểu diễn cho độ lớn vectơ cường độ điện trường \(E=\dfrac{10^{-10}}{6\pi\varepsilon_0}\) (V/m). Hãy tính và vẽ vectơ cường độ điện trường tại một điểm cách Q một khoảng 2 cm và 3 cm.
Thảo luận (1)Hướng dẫn giảiĐoạn thẳng 1cm biểu diễn cho độ lớn của cường độ điện trường \(E = \frac{{{{10}^{ - 10}}}}{{6\pi {\varepsilon _0}}} = 0,6\)V/m.
Cường độ điện trường tại điểm cách Q một khoảng 2 cm:
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{\left| {{{6.10}^{ - 14}}} \right|}}{{4\pi 8,{{85.10}^{ - 12}}.0,{{02}^2}}} = 1,34\)V/m
Vectơ cường độ điện trường:
Cường độ điện trường tại điểm cách Q một khoảng 3 cm:
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{\left| {{{6.10}^{ - 14}}} \right|}}{{4\pi 8,{{85.10}^{ - 12}}.0,{{03}^2}}} = 0,6\)V/m
Vectơ cường độ điện trường:
(Trả lời bởi Hà Quang Minh)
Hãy chứng tỏ rằng: Độ lớn cường độ điện trường tại một điểm trong công thức (17.1) bằng độ lớn của lực điện tác dụng lên một đơn vị điện tích đặt tại điểm đó.
\(E=\dfrac{F}{q}\) (17.1)
Thảo luận (1)Hướng dẫn giảiĐộ lớn cường độ điện trường tại 1 điểm:
\(E=k\dfrac{\left|Q\right|}{r^2}\)
Lực điện tác dụng lên một đơn vị điện tích đặt tại điểm đó:
\(E=\dfrac{F}{q}=\dfrac{k\dfrac{\left|Q\cdot q\right|}{r^2}}{q}=k\dfrac{\left|Q\right|}{r^2}\)
Chứng tỏ: Độ lớn cường độ điện trường tại một điểm bằng độ lớn của lực điện tác dụng lên một đơn vị điện tích đặt tại điểm đó.
(Trả lời bởi HT.Phong (9A5))
Một điện tích điểm Q = 6.10 -13 C đặt trong chân không.
a) Xác định phương, chiều, độ lớn của cường độ điện trường do điện tích điểm Q gây ra tại một điểm cách nó một khoảng 1 cm, 2 cm, 3 cm.
b) Nhận xét về cường độ điện trường ở những điểm gần điện tích Q và ở những điểm cách xa điện tích Q.
c) Từ các nhận xét trên, em hãy mô tả cường độ điện trường do một điện tích điểm dương Q đặt trong chân không gây ra tại một điểm cách nó một khoảng r. Vẽ hình minh hoạ.
Thảo luận (1)Hướng dẫn giảia) Phương của cường độ điện trường này trùng với đường nối của điện tích với điểm đang xét.
Chiều của cường độ điện trường hướng ra xa điện tích (do Q là điện tích dương).
Độ lớn của cường độ điện trường do điện tích điểm Q gây ra tại một điểm cách nó một khoảng 1 cm là:
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{{{3.10}^{ - 9}}}}{{2\pi {\varepsilon _0}}}\)(V/m)
Độ lớn của cường độ điện trường do điện tích điểm Q gây ra tại một điểm cách nó một khoảng 2 cm là
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{{{15.10}^{ - 10}}}}{{4\pi {\varepsilon _0}}}\) (V/m)
Độ lớn của cường độ điện trường do điện tích điểm Q gây ra tại một điểm cách nó một khoảng 3 cm là
\(E = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{{{5.10}^{ - 10}}}}{{3\pi {\varepsilon _0}}}\) (V/m)
b) Càng gần điện tích thì cường độ điện trường càng mạnh, càng xa điện tích thì cường độ điện trường càng yếu. Phù hợp với công thức thể hiện mối quan hệ giữa cường độ điện trường và khoảng cách từ điện tích đến điểm xét: độ lớn cường độ điện trường tỉ lệ nghịch với bình phương khoảng cách từ điện tích đến điểm xét.
c) Cường độ điện trường do một điện tích điểm dương gây ra có:
- Phương: trùng với đường nối của điện tích với điểm đang xét.
- Chiều: hướng ra xa điện tích.
- Độ lớn: tỉ lệ nghịch với bình phương khoảng cách từ điện tích điểm đó đến điểm xét.
(Trả lời bởi Hà Quang Minh)
Nếu trong không gian có hai điện tích điểm dương Q1 = Q2 được đặt ở hai điểm B và C, một điện tích thử q được đặt tại một điểm A như Hình 17.4. Hãy mô tả bằng hình vẽ lực điện tổng hợp do Q1 và Q2 tác dụng lên điện tích thử q.
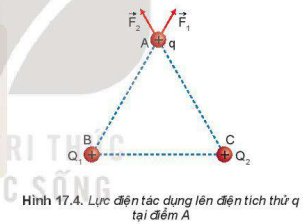
Thảo luận (1)Hướng dẫn giải
Đặt điện tích điểm Q1 = 6.10-8 C tại điểm A và điện tích điểm Q2 = - 2.10-8 C tại điểm B cách A một khoảng bằng 3 cm (Hình 17.5). Hãy xác định những điểm mà cường độ điện trường tại đó bằng 0.
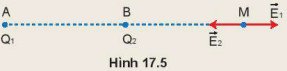
Thảo luận (1)Hướng dẫn giảiCường độ điện trường bằng 0 khi:
\(\overrightarrow {{E_1}} + \overrightarrow {{E_2}} = \overrightarrow {{E_3}} = \overrightarrow 0 \Rightarrow \overrightarrow {{E_1}} = - \overrightarrow {{E_2}} \)
\( \Rightarrow \left\{ \begin{array}{l}{E_1} \uparrow \downarrow {E_2}\\{E_1} = {E_2}\end{array} \right.\)
Vì |q1| > |q2| ⇒ Điểm đó thuộc đường thẳng AB và ngoài đoạn AB, gần B hơn (r1>r2)
\( \Rightarrow \left\{ \begin{array}{l}{r_1} - {r_2} = AB\\\frac{{r_1^2}}{{r_2^2}} = \frac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}}\end{array} \right. \Rightarrow {r_1} = 0,071m;{r_2} = 0,041m\)
Vậy điểm cần tìm cách A 7,1 cm và cách B 4,1 cm.
(Trả lời bởi Hà Quang Minh)
Cho tam giác ABC vuông tại A có AB = 3 cm và AC = 4 cm. Tại điểm B ta đặt điện tích Q1 = 4,5.10-8 C, tại điểm C ta đặt điện tích Q2 = 2.10-8 C
a) Tính độ lớn của cường độ điện trường do mỗi điện tích trên gây ra tại A.
b) Tính cường độ điện trường tổng hợp tại A.
Thảo luận (1)Hướng dẫn giảia) Cường độ điện trường do điện tích Q1 gây ra tại A là:
\(E_1=\dfrac{\left|Q_1\right|}{4\pi\varepsilon_0AB^2}=\dfrac{5\cdot10^{-5}}{4\pi\varepsilon_0}\)(V/m)
Cường độ điện trường do điện tích Q2 gây ra tại A là:
\(E_2=\dfrac{\left|Q_2\right|}{4\pi\varepsilon_0AC^2}=\dfrac{25\cdot10^{-6}}{4\pi\varepsilon_0}\)(V/m)
b) Mà ta có:
\(E_1\perp E_2\Rightarrow E=\sqrt{E^2_1+E^2_2}=463427\left(V/m\right)\)
(Trả lời bởi HT.Phong (9A5))
Một hạt bụi mịn loại pm2,5 có điện tích bằng 1,6.10-19 C lơ lửng trong không khí nơi có điện trường của Trái Đất bằng 120 V/m. Bỏ qua trọng lực, tính lực điện của Trái Đất tác dụng lên hạt bụi mịn và từ đó giải thích lí do hạt bụi loại này thường lơ lửng trong không khí.
Thảo luận (1)Hướng dẫn giảiTham khảo:
Ta có: Lực điện tác dụng vào hạt bụi trong điện trường là:
\(F=E\cdot q=120\cdot1,6\cdot10^{-19}=1,92\cdot10^{-17}N\)
Vì hạt bụi mịn có điện tích dương nên lực điện sé có chiều theo chiều điện trường, tức là hướng từ trên xuống dưới mặt đất. Lực điện này là một trong những nguyên nhân làm cho các hạt bụi mịn không bị gió cuỗn bay lên cao được.
(Trả lời bởi HT.Phong (9A5))