Cho tứ diện ABCD có tất cả các cạnh đều bằng a, gọi M là trung điểm của AB. Mặt phẳng (P) qua M song song với mp(BCD) cắt tứ diện theo 1 thiết diện là
tam giác đều.tam giác vuông.hình thang.hình bình hành.Hướng dẫn giải: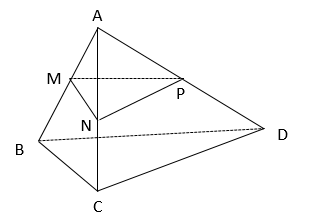
Trong mp(ABC) từ M, kẻ MN // BC, suy ra N là trung điểm của AC.
Trong mp(ACD) từ N, kẻ NP // DC, suy ra P là trung điểm của AD.
Theo định nghĩa đường trung bình trong một tam giác ta có:
\(MN=\dfrac{1}{2}BC,NP=\dfrac{1}{2}CD,MP=\dfrac{1}{2}BD\).
Do BC = CD = BD nên MN = NP = PM hay tam giác MNP đều.

