Cho tam giác ABC vuông vân tại B. Trên cạnh AB lấy điểm H, trên tia đối của tia BC lấy điểm C sao cho BH=BD. Gọi I là giao điểm của DH và AC. Chọn khẳng định ĐÚNG.
DH vuông góc với AC.Góc CDI bằng 600.DH vuông góc với AB.Tam giác HDB đều.Hướng dẫn giải: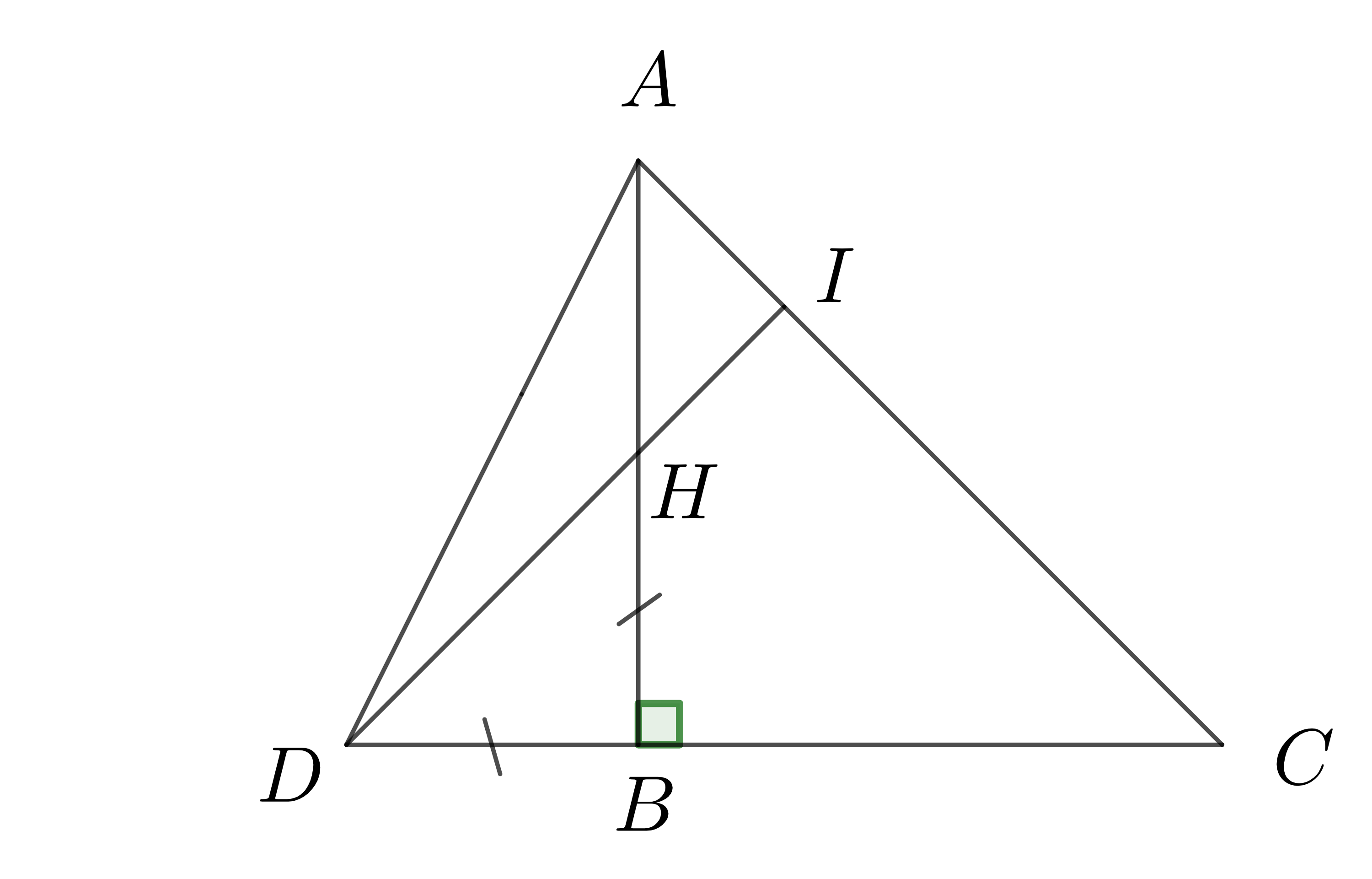
Do tam giác ABC vuông cân tại B nên \(\widehat{C}=45^0\)
Mặt khác tam giác BHD vuông cân tại B (do BH=BD) nên \(\widehat{BDH}=45^0\)
Hay \(\widehat{CDI}=45^0\)
Xét tam giác CDI có: \(\widehat{CDI}+\widehat{DCI}+\widehat{CID}=180^0\)
\(\Rightarrow45^0+45^0+\widehat{CID}=180^0\)
\(\Rightarrow\widehat{CID}=90^0\)
Nên DH vuông góc với AC.

