Cho tam giác ABC, điểm I nằm trong tam giác. Các tia AI,BI,CI cắt các cạnh BC,AC,AB lần lượt tại D,E,F. Tổng \(\dfrac{AF}{FB}+\dfrac{AE}{EC}\) bằng tỉ số nào dưới đây?
\(\dfrac{AI}{AD}\).\(\dfrac{AI}{ID}\).\(\dfrac{BD}{DC}\).\(\dfrac{DC}{DB}\).Hướng dẫn giải: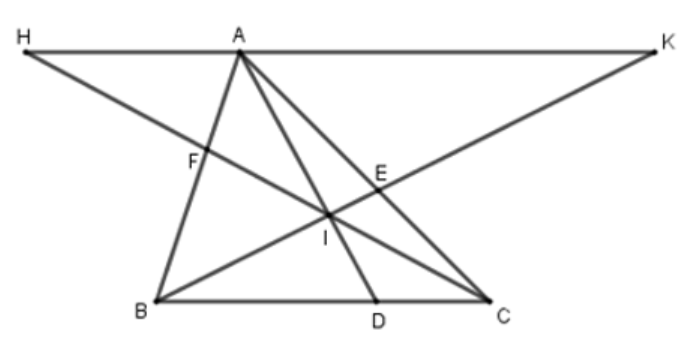
Qua A kẻ đường thẳng song song với BC cắt CF,BE tại H,K.
Do AH//BC nên theo định lí Talet ta có: \(\dfrac{AF}{FB}=\dfrac{AH}{BC}\)
Do AK//BC nên theo định lí Talet ta có: \(\dfrac{AE}{EC}=\dfrac{AK}{BC}\)
Suy ra \(\dfrac{AF}{FB}+\dfrac{AE}{EC}=\dfrac{AH}{BC}+\dfrac{AK}{BC}=\dfrac{HK}{BC}\) (1)
Lại có: AH//DC nên theo định lí Talet ta có: \(\dfrac{AI}{ID}=\dfrac{AH}{DC}\)
AK//BD nên theo định lí Talet ta có: \(\dfrac{AI}{ID}=\dfrac{AK}{BD}\)
\(\Rightarrow\) \(\dfrac{AI}{ID}=\dfrac{AH}{DC}=\dfrac{AK}{BD}=\dfrac{AH+AK}{DC+BD}=\dfrac{HK}{BC}\) (2)
Từ (1) và (2) suy ra \(\dfrac{AF}{FB}+\dfrac{AE}{EC}=\dfrac{AI}{ID}\)

