Cho tam giác ABC cân tại A. Trên cạnh AB, AC lấy điểm P, Q sao cho AP = AQ. Gọi O là giao điểm CP và BQ. Khi đó
OB = OC.O cách đều 2 cạnh AB, AC.Tam giác OBC cân.Tất cả đều đúng.Hướng dẫn giải: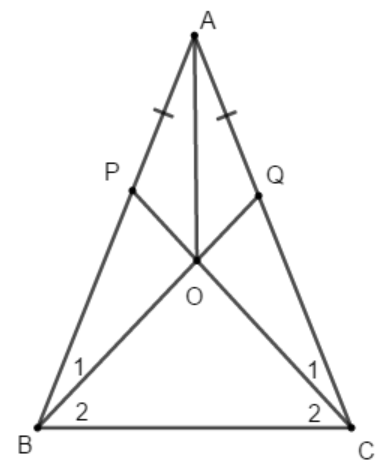
Xét tam giác ABQ và tam giác ACP có: AB=AC ; \(\widehat{A}\) chung ; AQ=AP
\(\Rightarrow\Delta ABQ=\Delta ACP\left(c.g.c\right)\)
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\) (hai góc tương ứng)
Mà \(\widehat{ABC}=\widehat{ACB}\) (do tam giác ABC cân tại A)
\(\Rightarrow\widehat{ABC}-\widehat{B_1}=\widehat{ACB}-\widehat{C_1}\) \(\Rightarrow\widehat{B_2}=\widehat{C_2}\)
\(\Delta OBC\) có \(\widehat{B_2}=\widehat{C_2}\) nên \(\Delta OBC\) cân tại O
\(\Rightarrow OB=OC\)
Khi đó ta chứng minh được \(\Delta AOB=\Delta AOC\left(c.c.c\right)\)
\(\Rightarrow\widehat{OAB}=\widehat{OAC}\) (hai góc tương ứng)
\(\Rightarrow AO\) là tia phân giác của góc BAC
Nên O cách đều AB, AC.

