Cho \(\left(O_1;3cm\right)\) tiếp xúc với \(\left(O_2;1cm\right)\) tại \(A\) sao cho điểm \(A\) nằm giữa \(O_1O_2\). Vẽ bán kính \(O_1B;O_2C\) song song nhau và thuộc cùng một nửa mặt phẳng bờ \(O_1O_2\). Kéo dài \(BC\) cắt \(O_1O_2\) tại \(D\). Độ dài \(O_1D\) là
\(4,5cm\)\(5cm\)\(8cm\)\(6cm\)Hướng dẫn giải: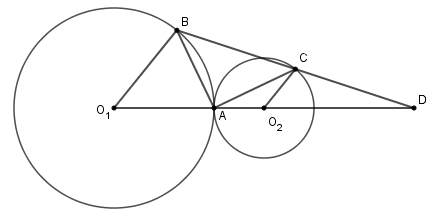
\(O_1B\) song song \(O_2C\) nên theo hệ quả định lí Ta-let ta có: \(\dfrac{O_2D}{O_1D}=\dfrac{O_2C}{O_1B}=\dfrac{1}{3}\)
\(\Rightarrow O_1D=\dfrac{3}{2}O_1O_2\).
Do hai đường tròn tiếp xúc nhau tại \(A\) nên \(A\in O_1O_2\Rightarrow O_1O_2=O_1A+O_2A=1+3=4\)
\(\Rightarrow O_1D=\dfrac{3}{2}.4=6\left(cm\right)\).

