Cho hình chóp tam giác đều \(S.ABC\) có các mặt bên đều là tam giác đều, đường cao \(SH\) . Biết \(HC=2\sqrt{3}cm\). Tính diện tích xung quanh của hình chóp.
\(18\sqrt{3}cm^2\).\(9\sqrt{3}cm^2\).\(27\sqrt{3}cm^2\).\(27cm^2\).Hướng dẫn giải: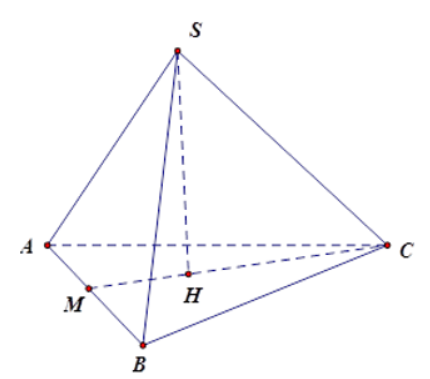
H là tâm đường tròn ngoại tiếp \(\Delta ABC\) đều nên H cũng là trọng tâm tam giác
CH cắt AB tại M thì AM=BM và \(CM\perp AB\)
Do H là trọng tâm tam giác nên \(CH=\dfrac{2}{3}CM\) \(\Rightarrow CM=3\sqrt{3}\left(cm\right)\)
Đặt AB=BC=AC=x(cm), AM=BM=x/2 (cm)
Áp dụng Pytago trong tam giác vuông MBC có: MB2+MC2=BC2
\(\Rightarrow x^2=\left(\dfrac{x}{2}\right)^2+\left(3\sqrt{3}\right)^2\)
Suy ra \(x=6\)
Do đó, tam giác SAB và ABC đều là các tam giác đều cạnh 6cm nên đường cao SM=CM=\(3\sqrt{3}\left(cm\right)\)
Suy ra hình chóp có cạnh đáy 6cm, trung đoạn \(3\sqrt{3}\left(cm\right)\)
Nên diện tích xung quanh hình chóp là: Sxq = \(\dfrac{1}{2}.6.3.3\sqrt{3}=27\sqrt{3}\left(cm^2\right)\)

