Cho \(\Delta ABC\) nhọn, đường cao \(BD\) và \(CE\). Vẽ các đường cao \(DF\) và \(EG\) của tam giác \(\Delta ADE\).
Xét các cặp tam giác sau, có mấy cặp tam giác đồng dạng?
(I) \(\Delta AEG\) và \(\Delta ABD\)
(II) \(\Delta ADF\) và \(\Delta ACE\)
(III) \(\Delta ABC\) và \(\Delta AEC\)
0.1.2.3.Hướng dẫn giải: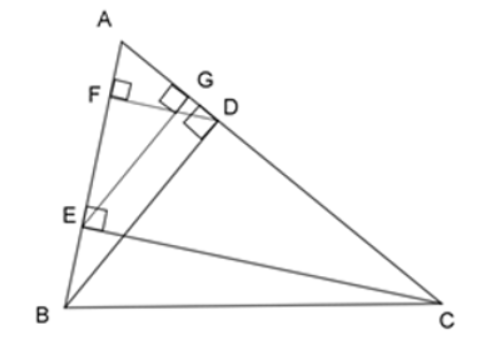
+) Xét \(\Delta AEG\) và \(\Delta ABD\) có:
\(BD\perp AC\) , \(EG\perp BC\) \(\Rightarrow\) BD//EG
Theo hệ quả của định lí Talet ta có: \(\dfrac{AE}{AB}=\dfrac{AG}{AD}=\dfrac{EG}{BD}\)
\(\Rightarrow\) \(\Delta AEG\) đồng dạng với \(\Delta ABD\) (c.c.c). Nên (I) đúng.
+) Chứng minh tương tự ta cũng được \(\Delta ADF\) đồng dạng với \(\Delta ACE\). nên (II) đúng
+) Ta thấy \(\dfrac{AE}{AB}\ne\dfrac{AC}{AC}\) nên \(\Delta ABC\) không đồng dạng với \(\Delta AEC\). Nên (III) sai.

