Cho ΔABC ∽ ΔDEF. Biết \(\widehat A = {60^o};\widehat E = {80^o}\), hãy tính số đo các góc \(\widehat B,\widehat C,\widehat D,\widehat E\)
Luyện tập chung trang 91
Bài 9.11 (SGK Kết nối tri thức với cuộc sống - Trang 92)
Thảo luận (1)
Bài 9.12 (SGK Kết nối tri thức với cuộc sống - Trang 92)
Cho ΔABC ∽ ΔA'B'C'. Biết AB=3cm, A′B′=6cm và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C'
Thảo luận (1)Hướng dẫn giảiCó \(\frac{{AB}}{{A'B'}} = \frac{3}{6} = \frac{1}{2}\)
=> ΔABC ∽ ΔA'B'C' với tỉ số đồng dạng là \(\frac{1}{2}\)
=> Chu vi tam giác ABC bằng \(\frac{1}{2}\) chu vi tam giác A'B'C'
=> Chu vi A'B'C' là: 2.10=20 (cm)
(Trả lời bởi Hà Quang Minh)
Bài 9.13 (SGK Kết nối tri thức với cuộc sống - Trang 92)
Cho hình thang ABCD (AB // CD) có \(\widehat {DAB} = \widehat {DBC}\)
a) Chứng minh rằng ΔABD ∽ ΔBDC
b) Giả sử AB=2cm,AD=3cm,BD=4cm. Tính độ dài các cạnh BC và DC
Thảo luận (1)Hướng dẫn giảia) Có AB // CD => \(\widehat {AB{\rm{D}}} = \widehat {B{\rm{D}}C}\)
- Xét ΔABD và ΔBDC
Có \(\widehat {AB{\rm{D}}} = \widehat {B{\rm{D}}C}{,^{}}\widehat {DAB} = \widehat {DBC}\)
=> ΔABD ∽ ΔBDC (g.g)
b) Có \(\frac{{AB}}{{B{\rm{D}}}} = \frac{{12}}{{24}} = \frac{1}{2}\)
ΔABD ∽ ΔBDC với tỉ số \(\frac{1}{2}\)
=> \(\frac{3}{{BC}} = \frac{4}{{DC}} = \frac{1}{2}\)
=> BC=6 (cm)
DC=8 (cm)
(Trả lời bởi Hà Quang Minh)
Bài 9.14 (SGK Kết nối tri thức với cuộc sống - Trang 92)
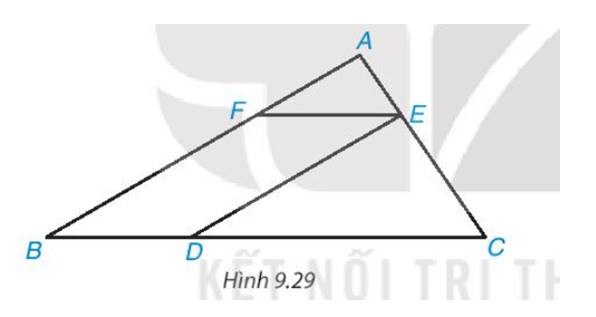
Cho các điểm A, B, C, D, E, F như Hình 9.29. Biết rằng DE // AB, EF // BC, DE=4cm, AB=6cm. Chứng minh rằng ΔAEF ∽ ΔECD và tính tỉ số đồng dạng
Thảo luận (1)Hướng dẫn giải- Có EF // BC => \(\widehat {{\rm{AEF}}} = \widehat {AC{\rm{D}}}\) (2 góc đồng vị) (1)
- Có EF // BD (vì EF // BC)
DE // FB (vì MN // BC)
=> EFBD là hình bình hành
=> \(\widehat {EFB} = \widehat {E{\rm{D}}B}\)
mà \(\widehat {EFB} + \widehat {{\rm{AEF}}} = {180^o}\)
\(\widehat {E{\rm{D}}B} + \widehat {E{\rm{D}}C} = {180^o}\)
=> \(\widehat {AF{\rm{E}}} = \widehat {E{\rm{D}}C}\) (2)
Từ (1) và (2) => ΔAEF ∽ ΔECD (g.g)
Có \(\frac{{AF}}{{E{\rm{D}}}} = \frac{2}{4} = \frac{1}{2}\)
=> Đồng dạng với tỉ số \(\frac{1}{2}\)
(Trả lời bởi Hà Quang Minh)
Bài 9.15 (SGK Kết nối tri thức với cuộc sống - Trang 92)
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat {BAC} = \widehat {C{\rm{D}}B}\). Chứng minh rằng ΔAED ∽ ΔBEC.
Thảo luận (1)Hướng dẫn giảiXét hai tam giác AEB và DEC có:
\(\widehat {BAC} = \widehat {C{\rm{D}}B}\)(giả thiết)
\(\widehat {AEB} = \widehat {DEC}\) (đối đỉnh)
Suy ra \(\Delta A{\rm{E}}B \backsim \Delta DEC\) suy ra: \(\frac{{A{\rm{E}}}}{{DE}} = \frac{{BE}}{{CE}} \Rightarrow \frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
Xét hai tam giác AED và BEC có:
\(\widehat {A{\rm{ED}}} = \widehat {BEC}\) (đối đỉnh)
\(\frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
Suy ra ΔAED ∽ ΔBEC (g – c – g)
(Trả lời bởi Hà Quang Minh)
Bài 9.16 (SGK Kết nối tri thức với cuộc sống - Trang 92)
Cho hình thang ABCD và các điểm M, N lần lượt trên cạnh AD và BC sao cho 2AM=MD, 2BN=NC. Biết AB=5cm,CD=6cm. Hãy tính độ dài đoạn thẳng MN
Thảo luận (1)Hướng dẫn giảiVì 2AM=MD suy ra \(\frac{{AM}}{{M{\rm{D}}}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{A{\rm{D}}}} = \frac{1}{3}\)
Vì 2BN=NC suy ra \(\frac{{BN}}{{NC}} = \frac{1}{2} \Rightarrow \frac{{NC}}{{CB}} = \frac{2}{3}\)
Xét hình thang ABCD có \(\frac{{AM}}{{M{\rm{D}}}} = \frac{{BN}}{{NC}}\) suy ra MN // AB //DC
Xét hai tam giác AMI và ADC có: góc A chung, \(\widehat {AIM} = \widehat {AC{\rm{D}}}\) (do MN// DC)
Suy ra \(\Delta AMI \backsim \Delta A{\rm{D}}C\) suy ra: \(\frac{{AM}}{{{\rm{AD}}}} = \frac{{MI}}{{DC}} = \frac{1}{3} \Rightarrow MI = \frac{1}{3}.DC = \frac{1}{3}.6 = 2(cm)\)
Xét hai tam giác CNI và CBA có góc A chung, \(\widehat {CIN} = \widehat {CAB}\) (do MN // AB)
Suy ra \(\Delta CNI \backsim \Delta CBA\) suy ra: \(\frac{{CN}}{{CB}} = \frac{{NI}}{{BA}} = \frac{2}{3} \Rightarrow NI = \frac{2}{3}.BA = \frac{2}{3}.5 = \frac{{10}}{3}\)(cm)
MN = MI + IN = \(2 + \frac{{10}}{3} = \frac{{16}}{3}(cm)\)
(Trả lời bởi Hà Quang Minh)