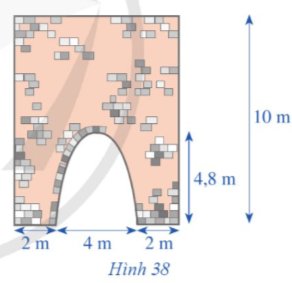
Hình 38 minh họa mặt cắt đứng của một bức tường cũ có dạng hình chữ nhật với một cổng ra vào có dạng hình parabol với các kích thước được cho như trong hình đó. Người ta dự định sơn lại mặt ngoài của bức tường đó. Chi phí để sơn bức tường là 15 000 đồng/1 m2. Tổng chi phí để sơn lại toàn bộ mặt ngoài của bức tường đó sẽ là bao nhiêu?