Bài 8: Tính chất ba đường trung trực của tam giác
Nội dung lý thuyết
Các phiên bản khác1. Đường trung trực của tam giác
- Trong một tam giác, đường trung trực của mỗi cạnh được gọi là đường trung trực của tam giác đó.
Cụ thể: Trong hình vẽ dưới đây, đường thẳng \(a\) là đường trung trực ứng với cạnh \(BC\) của tam giác \(ABC\):

Tương tự ta cũng có các đường thẳng \(b,c\) lần lượt là các đường trung trực ứng với cạnh \(AC,AB\) của tam giác \(ABC\):

Như vậy, mỗi tam giác có 3 đường trung trực.
Nhận xét: Trong một tam giác, đường trung trực của một cạnh không nhất thiết phải đi qua đỉnh đối diện với cạnh ấy. Tuy nhiên, trong một tam giác cân, đường trung trực của cạnh đáy luôn đi qua đỉnh đối diện với cạnh ấy.
Tính chất:
Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh này.

@1789277@
2. Tính chất ba đường trung trực của tam giác
Định lí:
Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác.
Ta có thể chứng minh định lí này bằng cách sau: Gọi \(O\) là giao điểm của hai đường trung trực ứng với cạnh \(AB\) và \(AC\) của tam giác \(ABC\). Ta sẽ chứng minh \(O\) cũng nằm trên đường trung trực của cạnh \(BC\) của tam giác đó và \(OA=OB=OC\).
| GT | \(\Delta ABC\) \(b\) là đường trung trực của \(AC\) \(c\) là đường trung trực của \(AB\) \(b\) và \(c\) cắt nhau tại \(O\) |
| KL | \(O\) nằm trên đường trung trực của \(BC\) \(OA=OB=OC\) |
Chứng minh:
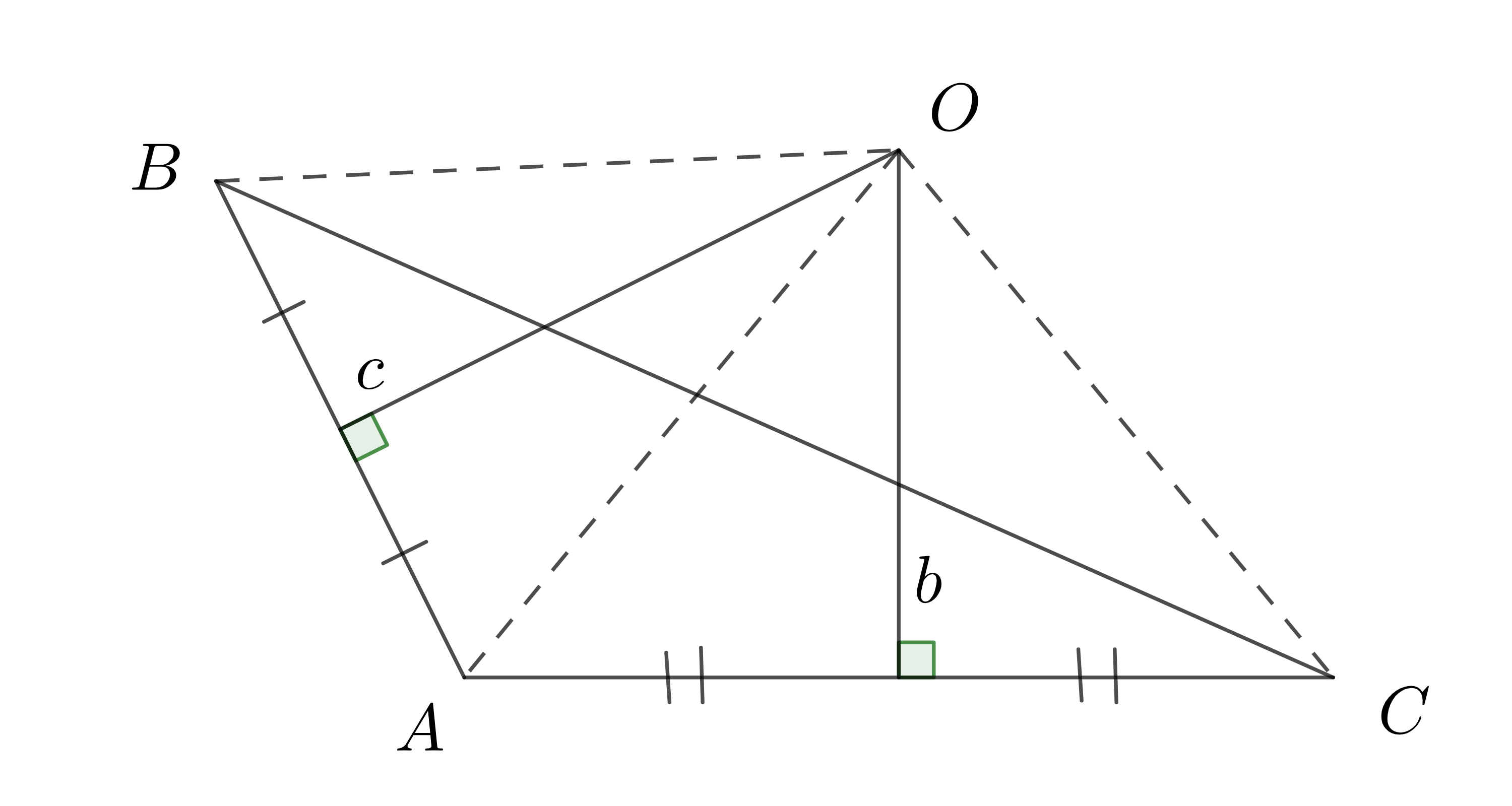
Vì \(O\) nằm trên đường trung trực \(b\) của đoạn thẳng \(AC\) nên
\(OA=OC\) (1)
Vì \(O\) nằm trên đường trung trực \(c\) của đoạn thẳng \(AB\) nên
\(OA=OB\) (2)
Từ (1) và (2) suy ra \(OB=OC\left(=OA\right)\)
do đó \(O\) nằm trên đường trung trực của đoạn thẳng \(BC\) (theo tính chất đường trung trực)
Vậy 3 đường trung trực của tam giác \(ABC\) cùng đi qua điểm \(O\) và ta có:
\(OA=OB=OC\)
- Chú ý: Vì giao điểm \(O\) của ba đường trung trực của tam giác \(ABC\) cách đều ba đỉnh của tam giác đó nên có một đường tròn tâm \(O\) đi qua ba đỉnh \(A,B,C\). Ta gọi đường tròn đó là đường tròn ngoại tiếp tam giác \(ABC\).
@1789049@