Bài 6: Từ vuông góc đến song song

1. Quan hệ giữa tính vuông góc với tính song song

Tính chất 1:

Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.

Ví dụ:

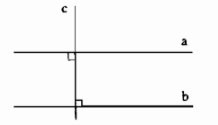
Ta có \(a\perp c\) và \(b\perp c\) nên \(a\) // \(b\)

Tính chất 2:

Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.

Ví dụ:

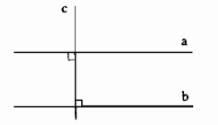
Ta có \(a\)//\(b\) và \(a\perp c\) nên \(b\perp c\)

Áp dụng các tính chất trên, ta xét một ví dụ sau: 

Cho \(BC\perp CD\) tại \(C\), \(AD\perp CD\) tại \(D\) (như hình vẽ), \(\widehat{DAB}=110^0\). Tính só đo góc \(\widehat{ABC}\).

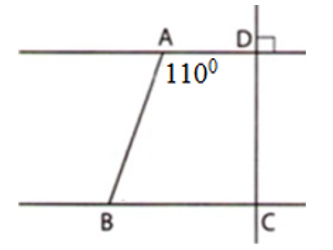
Ta có \(BC\perp CD\) mà  \(AD\perp CD\)  \(\Rightarrow\) \(AD\) // \(BC\) 

\(\Rightarrow\) \(\widehat{DAB}+\widehat{ABC}=180^0\) (hai góc trong cùng phía)

\(\Rightarrow\) \(\widehat{ABC}=180^0-\widehat{DAB}=180^0-110^0=70^0\) .

Vậy số đo góc \(\widehat{ABC}\) là \(70^0\).

2. Ba đường thẳng song song.

Ta có tính chất sau:

Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.

Ta có thể mô tả tính chất trên bởi ví dụ sau:

\(d\) // \(d'\) và \(d\) // \(d''\) \(\Rightarrow\) \(d'\) // \(d''\) 

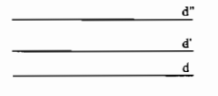
Khi đó, nếu có một đương fthẳng \(a\) sao cho \(a\perp d\)  thì \(a\perp d'\) và \(a\perp d''\).

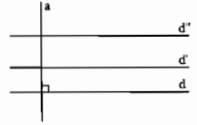
Chú ý: Khi ba đường thẳng \(d\),\(d'\),\(d''\) song song với nhau từng đôi một, ta nói ba đường thẳng đó song song với nhau và kí hiệu là \(d\)//\(d'\)//​\(d''\)​.

Xét ví dụ sau:

Cho hình vẽ sau. Biết \(AB\)//\(DE\). Tính \(\widehat{BCE}\)?

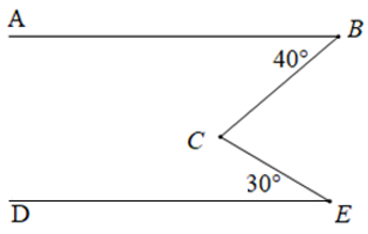
Bài làm: 

Trong góc \(BCE\) , vẽ \(CF\) // \(AB\).

\(\Rightarrow\) \(\widehat{ABC}=\widehat{BCF}=40^0\) (hai góc so le trong)

Lại có \(AB\)//\(DE\) mà \(CF\)//\(AB\) \(\Rightarrow\) \(CF\) // \(DE\) 

\(\Rightarrow\) \(\widehat{DEC}=\widehat{ECF}=30^0\) (hai góc so le trong)

Do \(CF\) nằm trong góc \(BCE\) nên \(\widehat{BCE}=\widehat{BCF}+\widehat{ECF}\)  \(\Rightarrow\) \(\widehat{BCE}=40^0+30^0=70^0\).

Vậy số đo góc \(BCE\) là \(70^0\).