Lý thuyết - Bài 5 Góc

I. KHÁI NIỆM GÓC

Góc là hình gồm hai tia chung gốc.

Trong hình bên:

Góc xOy (hoặc góc yOx) được kí hiệu là \(\widehat{xOy}\) (hoặc \(\widehat{yOx}\)).
Hai tia Ox và Oy được gọi là hai cạnh của góc. Gốc chung O của hai tia được gọi là đỉnh của góc.

Ví dụ. Hãy đọc và viết tên các góc đỉnh I ở hình dưới và chỉ ra các cạnh của chúng.

Giải:

Ta có các góc đỉnh I là: \(\widehat{BIC},\widehat{BIm},\widehat{CIm}.\)

Góc BIC có cạnh là IB và IC.
Góc BIm có cạnh là IB và Im.
Góc CIm có cạnh là IC và Im.

Để vẽ góc AIB, ta lần lượt vẽ các tia IA và IB. Khi đó, ta nhận được góc AIB có cạnh là IA và IB.

@599890@

II. ĐIỂM NẰM TRONG GÓC

Điểm M như trong hình dưới (không thuộc tia Ox, Oy) được gọi là điểm nằm trong góc xOy hay điểm trong của góc xOy.

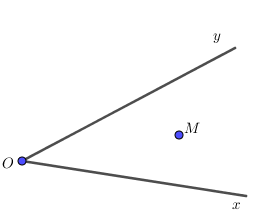
Ví dụ. Hãy kể tên các điểm nằm trong góc xOy, các điểm không nằm trong góc xOy ở hình dưới đây.

Giải:

Các điểm nằm trong góc xOy là M, E.

Các điểm không nằm trong góc xOy là D, H, Q.

@588375@

III. SỐ ĐO CỦA GÓC

1. Đo góc

Ta thường xác định số đo góc bằng thước đo góc.

Thước đo góc có dạng hình tròn và được chia đều thành 180 phần bằng nhau, mỗi phần ứng với 1^o.

Để xác định số đo của góc xOy bằng thước đo góc, ta làm như sau:

Bước 1. Đặt thước đo góc sao cho tâm của thước trùng với đỉnh của góc. Vạch 0 của thước nằm trên cạnh Ox

Bước 2. Xác định xem cạnh Oy đi qua vạch chia độ nào thì đó chính là số đo góc.

Trong hình bên ta quan sát được số đo của góc xOy bằng 60^o.

Mỗi góc có một số đo.

Chú ý:

Nếu số đo của góc xOy là n^o thì ta kí hiệu \(\widehat{xOy}=n^o\) hoặc \(\widehat{yOx}=n^o\).
Chúng ta chỉ xét các góc có số đo không vượt quá 180^o.

Ví dụ. Dùng thước đo góc để vẽ góc mOn có số đo bằng 100^o.

Giải:

Để vẽ góc mOn có số đo bằng 100^o, ta làm như sau:

Bước 1. Vẽ tia Ox

Bước 2.

Đặt thước đo góc sao cho tâm của thước trùng với O, vạch 0 của thước nằm trên tia Ox

Bước 3.

Đánh dấu một điểm trên vạch chia độ của thước tương ứng với số chỉ 100 độ, kẻ tia Oy đi qua điểm đã đánh dấu.

Khi đó ta có \(\widehat{xOy}=100^o\) đã được vẽ.

Chú ý:

Trong một hình có nhiều góc, người ta thường vẽ thêm một hay nhiều vòng cung nhỏ nối hai cạnh của góc đó để dễ thấy góc mà ta đang xét tới.
Khi cần phân biệt các góc có chung một đỉnh, chẳng hạn chung đỉnh O, ta dùng kí hiệu \(\widehat{O_1},\widehat{O_2}\).

2. So sánh hai góc

Cho góc xOy và mEn. Để so sánh hai góc, ta có thể dựa vào số đo của chúng.

Nếu số đo của góc xOy bằng số đo của góc mEn thì góc xOy bằng góc mEn và được kí hiệu là \(\widehat{xOy}=\widehat{mEn}\).
Nếu số đo của góc xOy lớn hơn số đo của góc mEn thì góc xOy lớn hơn góc mEn và được kí hiệu là \(\widehat{xOy}>\widehat{mEn}\).
Nếu số đo của góc xOy nhỏ hơn số đo của góc mEn thì góc xOy nhỏ hơn góc mEn và được kí hiệu là \(\widehat{xOy}< \widehat{mEn}\).

Ví dụ. Cho các góc \(\widehat{xOy}=95^o,\widehat{tOm}=70^o,\widehat{uPv}=40^o\).

a) So sánh hai góc xOy và tOm.

b) So sánh hai góc uPv và tOm.

Giải:

a) Vì \(\widehat{xOy}=95^o,\widehat{tOm}=70^o\) nên \(\widehat{xOy}>\widehat{tOm}\left(95^o>70^o\right)\) .

b) Vì \(\widehat{uPv}=40^o,\widehat{tOm}=70^o\) nên \(\widehat{uPv}< \widehat{tOm}\left(40^o< 70^o\right)\).

@589104@

IV. GÓC VUÔNG, GÓC NHỌN, GÓC TÙ, GÓC BẸT

Góc nhọn là góc có số đo lớn hơn 0^o và nhỏ hơn 90^o.
Góc vuông là góc có số đo bằng 90^o.
Góc tù là góc có số đo lớn hơn 90^o và nhỏ hơn 180^o.
Góc bẹt là góc có số đo bằng 180^o.

Ví dụ 1. Cho các góc \(\widehat{xOy}=90^o,\widehat{yOt}=120^o,\widehat{xOz}=35^o\). Khi đó ta có:

\(\widehat{xOy}\) là góc vuông vì \(\widehat{xOy}=90^o\).
\(\widehat{yOt}\) là góc tù vì \(\widehat{yOt}>90^o\).
\(\widehat{xOz}\) là góc nhọn vì \(\widehat{xOz}< 90^o\).

Ví dụ 2. Hình bên có bao nhiêu góc vuông, góc nhọn, góc tù, góc bẹt. Chỉ ra tên mỗi góc trong từng trường hợp.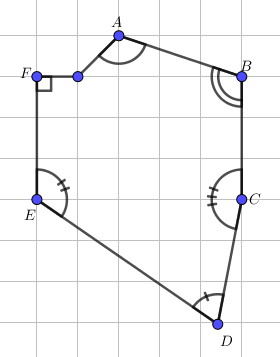

Giải:

Quan sát hình vẽ, ta thấy:

Chỉ có một góc vuông là góc F.
Có bốn góc tù là các góc A, B, C, E.
Có một góc nhọn là là góc D.
Không có góc bẹt nào.

@589184@

Bài 5. Góc