Bài tập cuối chương VI
Nội dung lý thuyết
1. Điểm
- Dấu chấm nhỏ trên giấy là hình ảnh của điểm
- Ta dùng chữ cái in hoa A, B, C, D, ... để đặt tên cho điểm
- Khi nói hai điểm mà không nói gì thêm, ta hiểu đó là hai điểm phân biệt
Chẳng hạn: Cho hai điểm A và B như hình bên.
2. Đường thẳng
- Đường thẳng không bị giới hạn về hai phía
- Ta dùng vạch thẳng để biểu diễn một đường thẳng
- Sử dụng những chữ cái in thường a, b, c, ... để đặt tên cho đường thẳng.
Ví dụ. Ta có đường thẳng a, b như hình dưới.
.png)
3. Điểm thuộc đường thẳng. Điểm không thuộc đường thẳng
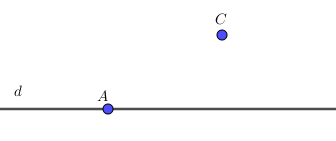
✽ Điểm A thuộc đường thẳng d còn được gọi là điểm A nằm trên đường thẳng d hay đường thẳng d đi qua điểm A, ta kí hiệu A ∈ d.
✽ Điểm C không thuộc đường thẳng d còn được gọi là điểm C không nằm trên đường thẳng d hay đường thẳng d không đi qua điểm C, ta kí hiệu A ∉ d.
Chú ý: Có vô số điểm thuộc một đường thẳng.
4. Đường thẳng đi qua hai điểm

✽ Đường thẳng đi qua hai điểm A, B còn được gọi là đường thẳng AB hay đường thẳng BA hay đường thẳng a.
✽ Có một và chỉ một đường thẳng đi qua hai điểm A và B.
5. Ba điểm thẳng hàng
- Khi ba điểm cùng thuộc một đường thẳng, ta nói chúng thẳng hàng.
- Khi ba điểm không cùng thuộc bất kì đường thẳng nào, ta nói chúng không thẳng hàng.
- Trong ba điểm thẳng hàng, có một và chỉ một điểm nằm giữa hai điểm còn lại.
Chẳng hạn: 
Trong hình bên, ba điểm M, P, Q thẳng hàng. Ba điểm M, N , P không thẳng hàng.
6. Hai đường thẳng cắt nhau. Hai đường thẳng song song
| Hai đường thẳng | cắt nhau | song song | trùng nhau |
| Định nghĩa | Hai đường thẳng chỉ có một điểm chung gọi là hai đường thẳng cắt nhau và điểm chung được gọi là giao điểm của hai đường đó. | Hai đường thẳng song song là hai đường thẳng không có điểm chung. | Hai đường thẳng trùng nhau là hai đường thẳng có vô số điểm chung. |
| Ví dụ | Hai đường thẳng x và y cắt nhau tại A. A chính là giao điểm của chúng.
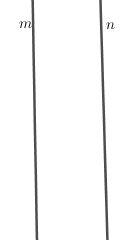
| Hai đường thẳng m và n song song với nhau.
| Hai đường thẳng MN và AB trùng nhau.
|
7. Đoạn thẳng
Đoạn thẳng AB là hình gồm điểm A, điểm B và tất cả các điểm nằm giữa A và B
- Đoạn thẳng AB cũng gọi là đoạn thẳng BA.
![]()
8. Độ dài đoạn thẳng
- Mỗi đoạn thẳng có độ dài là một số dương
- Hai đoạn thẳng bằng nhau thì có độ dài bằng nhau
- Độ dài của đoạn thẳng AB cũng được gọi là khoảng cách giữa hai điểm A và B
Chẳng hạn: Đoạn thẳng MN dài 10 cm.
.png)
9. Trung điểm của đoạn thẳng
- Trung điểm M của đoạn thẳng AB là điểm nằm giữa hai điểm A và B sao cho MA = MB.

- Nếu M là trung điểm của đoạn thẳng AB thì độ dài mỗi đoạn thẳng MA, MB đều bằng một nửa độ dài đoạn thẳng AB tức là \(MA=MB=\dfrac{AB}{2}\).
Ví dụ: Cho đoạn thẳng AB có độ dài bằng 20 cm và M là trung điểm. Khi đó \(MA=MB=\dfrac{AB}{2}=\dfrac{20}{2}=10\) cm.
10. Tia
Hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O.
Tia Ox thường được biểu diễn bằng một vạch thẳng có ghi rõ điểm gốc O như hình dưới. Tia Ox không bị giới hạn về phía x.

Chú ý: Cho tia gốc O và điểm A nằm trên tia gốc O. Khi đó ta đọc và viết là tia OA, không được đọc và viết là tia AO.
![]()
11. Hai tia đối nhau
Hai tia chung gốc Ox, Oy tạo thành đường thẳng xy được gọi là hai tia đối nhau.

Chẳng hạn:

Trong hình trên, ta có hai tia Hm và Hn đối nhau. Hai tia DH và Kn không đối nhau vì chúng ko có chung gốc.
12. Hai tia trùng nhau
- Lấy điểm A khác điểm O trên tia Ox. Tia Ox và tia OA là hai tia trùng nhau.
![]()
- Hai tia trùng nhau thì phải có chung điểm gốc.
Chẳng hạn: Hai tia AB và An trong hình sau là hai tia trùng nhau.
![]()
13. Góc
Góc là hình gồm hai tia chung gốc.
Trong hình bên, ta có:
✽ Góc AOB (hay góc BOA) được kí hiệu là \(\widehat{AOB}\) (hoặc \(\widehat{BOA}\)).
✽ Hai tia OA và OB là hai cạnh của góc, đỉnh là O.
14. Điểm nằm trong góc
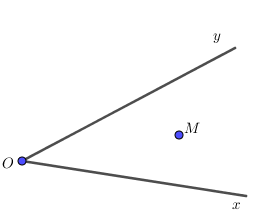
Điểm M trong hình trên (không thuộc tia Ox, Oy) được gọi là điểm nằm trong góc xOy hay điểm trong của góc xOy.
15. Góc vuông, góc nhọn, góc tù, góc bẹt
| Loại góc | Góc nhọn | Góc vuông | Góc tù | Góc bẹt |
| Định nghĩa | là góc có số đo lớn hơn 0o và nhỏ hơn 90o. | là góc có số đo bằng 90o. | là góc có số đo lớn hơn 90o và nhỏ hơn 180o. | là góc có số đo bằng 180o. |
| Ví dụ |  |  |  |  |
Chú ý: Số đo góc nhọn < góc vuông < góc tù < góc bẹt.