Bài 8: Vị trí tương đối của hai đường tròn (Tiếp)
Nội dung lý thuyết
Các phiên bản khác1. Hệ thức giữa đoạn nối tâm và các bán kính
Xét hai đường tròn \(\left(O;R\right)\) và \(\left(O';r\right)\) với giả thiết \(R>r\).
a) Hai đường tròn cắt nhau
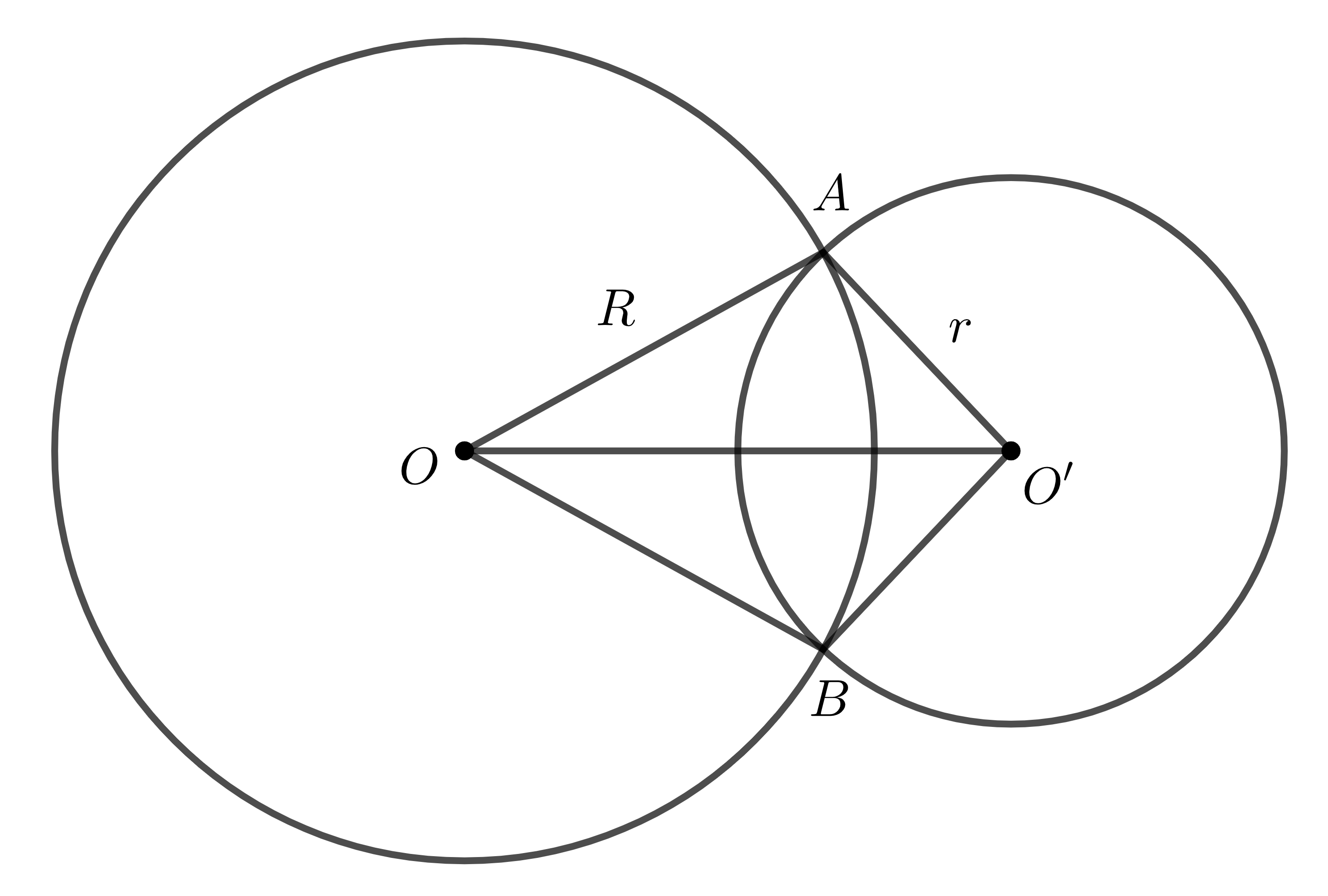
Giả sử hai đường tròn \(\left(O\right);\left(O'\right)\) cắt nhau tại hai điểm \(A,B\).
Khi đó, ba điểm \(A,O,O'\) không thẳng hàng nên tồn tại tam giác \(AOO'\). Theo bất đẳng thức tam giác, ta có: \(OO'< OA+O'A\)
\(\Rightarrow OO'< R+r\).
b) Hai đường tròn tiếp xúc nhau
+) Nếu hai đường tròn \(\left(O\right);\left(O'\right)\) tiếp xúc ngoài tại \(A\), ta có: điểm \(A\) nằm giữa \(O\) và \(O'\).
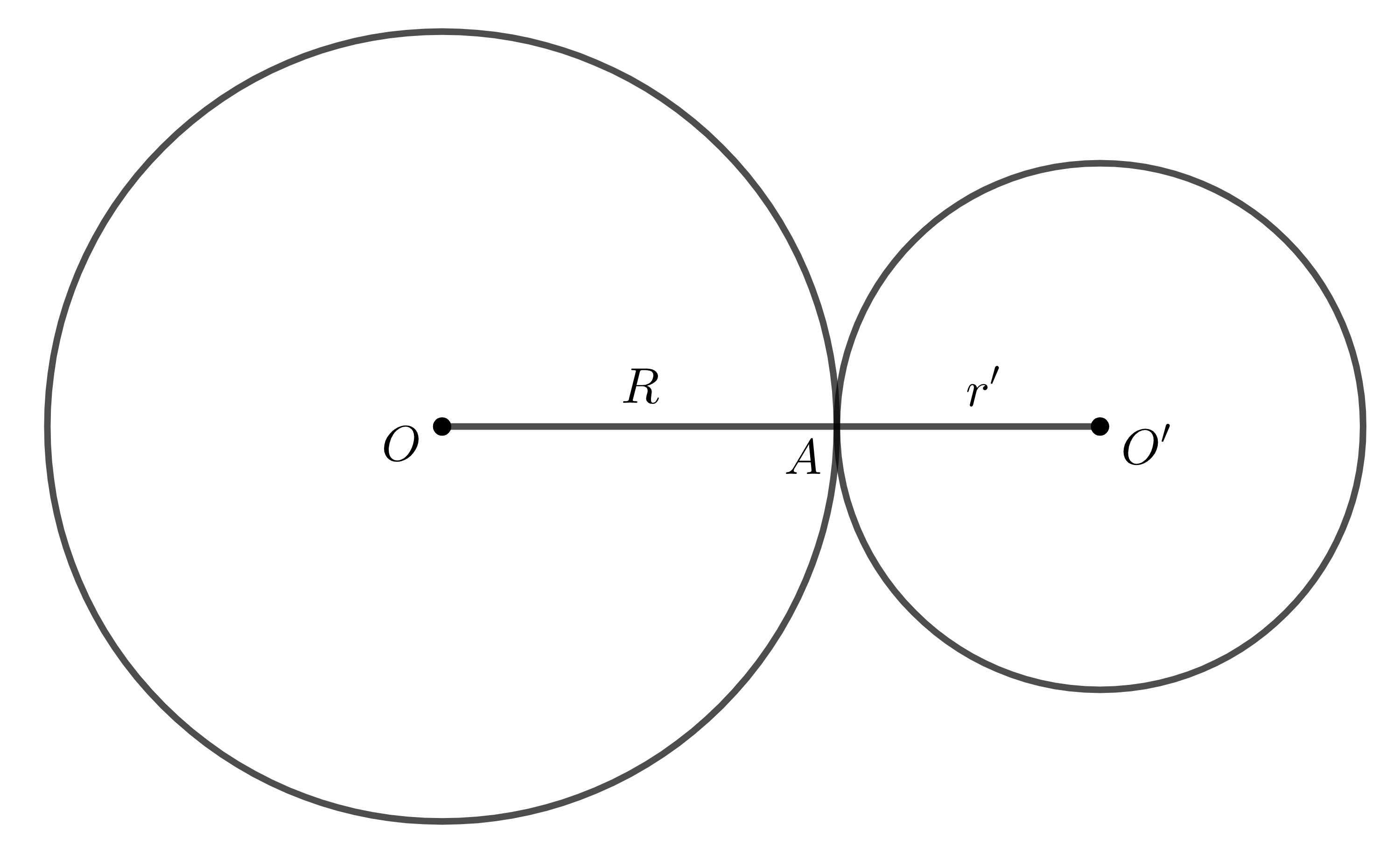
Khi đó, ta có: \(OO'=OA+O'A\Rightarrow OO'=R+r\).
+) Nếu hai đường tròn \(\left(O\right);\left(O'\right)\) tiếp xúc trong tại \(A\), ta có: điểm \(O'\) nằm giữa \(A\) và \(O\).

Khi đó, ta có: \(OO'=OA-O'A\Rightarrow OO'=R-r\).
c) Hai đường tròn không giao nhau
Hai đường tròn \(\left(O\right);\left(O'\right)\) không giao nhau có thể chia thành hai trường hợp:
+) \(\left(O\right);\left(O'\right)\) ở ngoài nhau:

Dễ thấy, trong trường hợp này: \(OO'>R+r\).
+) \(\left(O\right)\) đựng \(\left(O'\right)\):

Đặc biệt, trong hình b, khi \(O\equiv O'\), ta gọi hai đường tròn \(\left(O\right);\left(O'\right)\) là hai đường tròn đồng tâm.
Trong trường hợp này, dễ thấy: \(OO'>R-r\).
Ta cũng chứng minh được điều ngược lại của các khẳng định trên. Do đó, ta có bảng tổng kết:
Vị trí tương đối của hai đường tròn \(\left(O;R\right)\) và \(\left(O';r\right)\) với \(R>r\) | Số điểm chung | Hệ thức giữa \(OO'\) với \(R\) và \(r\) |
| Hai đường tròn cắt nhau | 2 | \(R-r< OO'< R+r\) |
Hai đường tròn tiếp xúc nhau - Tiếp xúc ngoài - Tiếp xúc trong | 1 |
\(OO'=R+r\) \(OO'=R-r>0\) |
Hai đường tròn không giao nhau - \(\left(O\right)\) và \(\left(O'\right)\) ở ngoài nhau - \(\left(O\right)\) đựng \(\left(O'\right)\) | 0 |
\(OO'>R+r\) \(OO'< R-r\) |
@423668@@423720@@57476@
2. Tiếp tuyến chung của hai đường tròn
Định nghĩa: Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó.
a) Hai đường tròn ở ngoài nhau
Hai đường tròn \(\left(O\right);\left(O'\right)\) ở ngoài nhau có 4 tiếp tuyến chung, chia thành hai trường hợp:
+) Các đường thẳng \(d_1;d_2\) là các tiếp tuyến chung ngoài của hai đường tròn (chúng không cắt đoạn nối tâm).
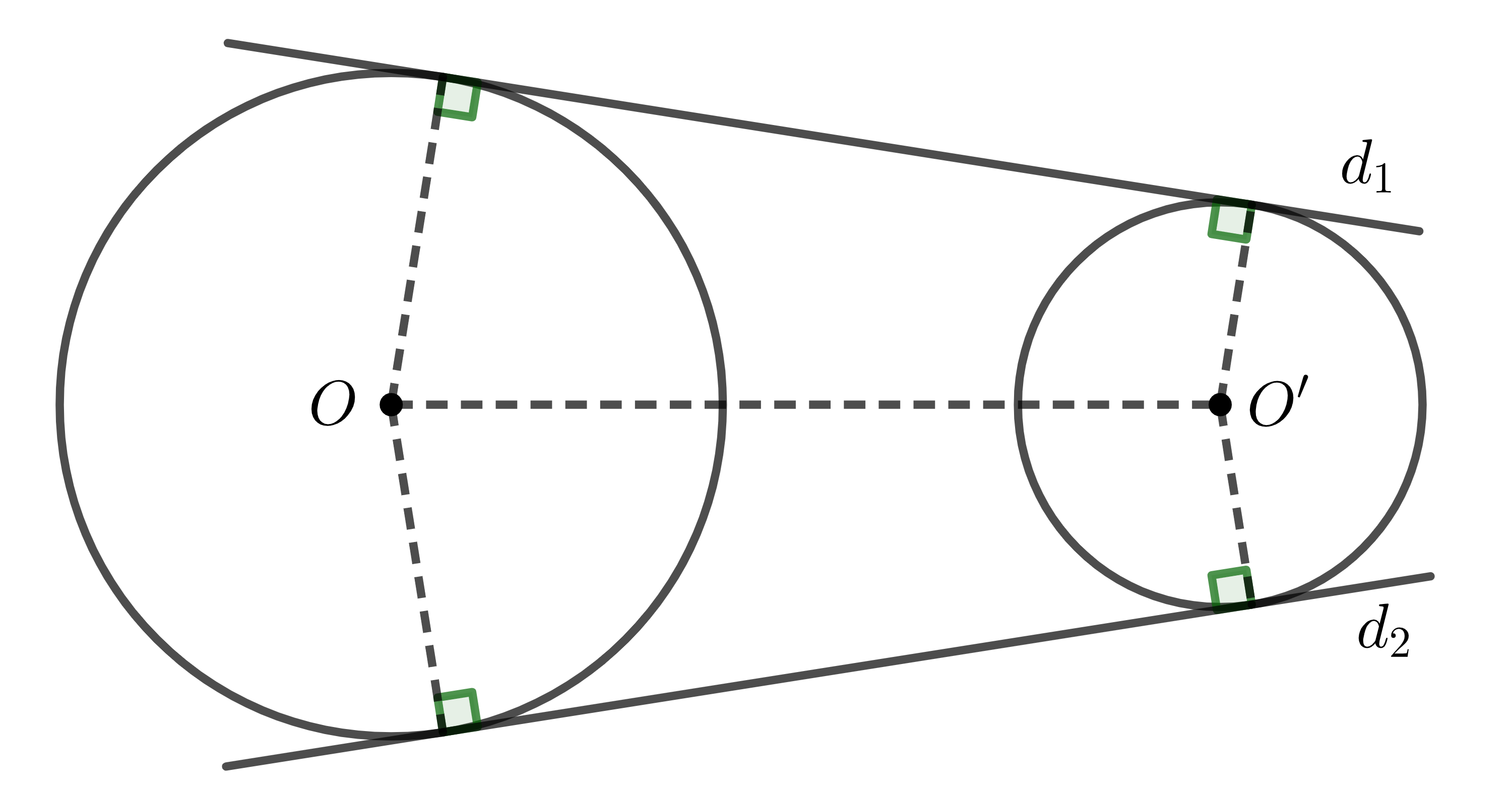
+) Các đường thẳng \(m_1;m_2\) là các tiếp tuyến chung trong của hai đường tròn (chúng cắt đoạn nối tâm).

b) Hai đường tròn tiếp xúc ngoài
Hai đường tròn \(\left(O\right);\left(O'\right)\) tiếp xúc ngoài nhau thì có 3 tiếp tuyến chung, trong đó \(d_1,d_2\) là các tiếp tuyến chung ngoài và \(m\) là tiếp tuyến chung trong.
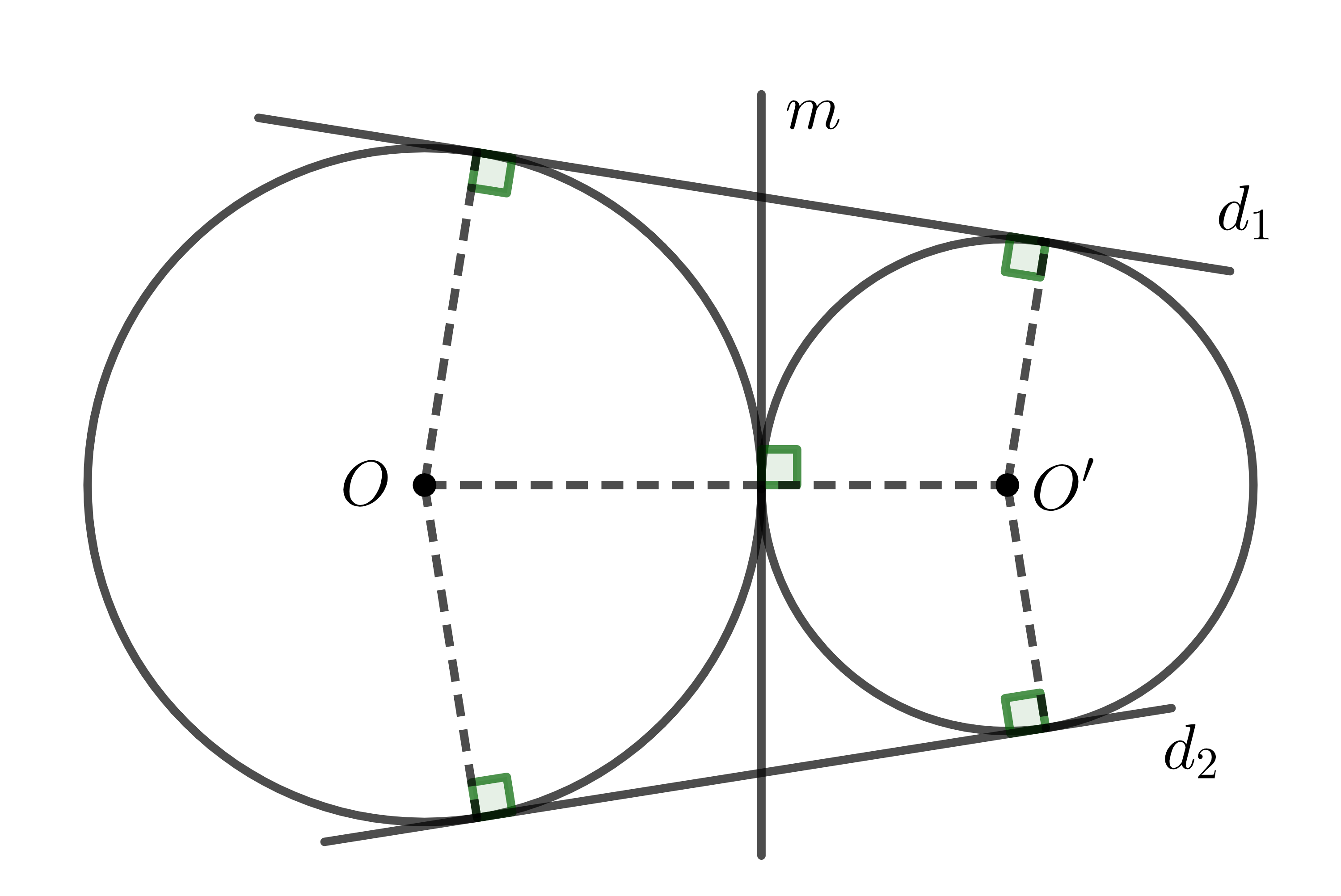
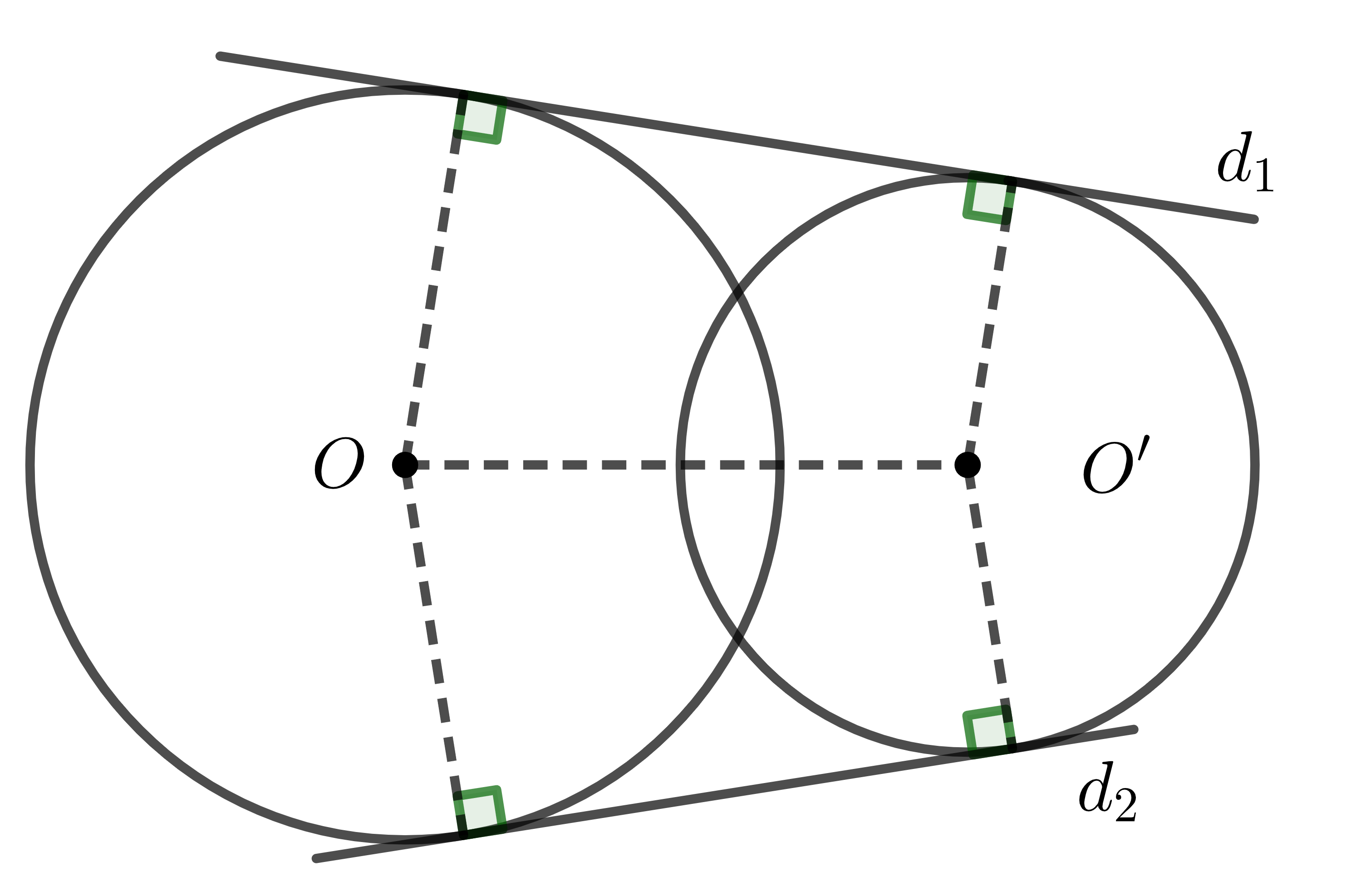
c) Hai đường tròn cắt nhau
Hai đường tròn \(\left(O\right);\left(O'\right)\) cắt nhau thì có 2 tiếp tuyến chung là các đường \(d_1,d_2\).
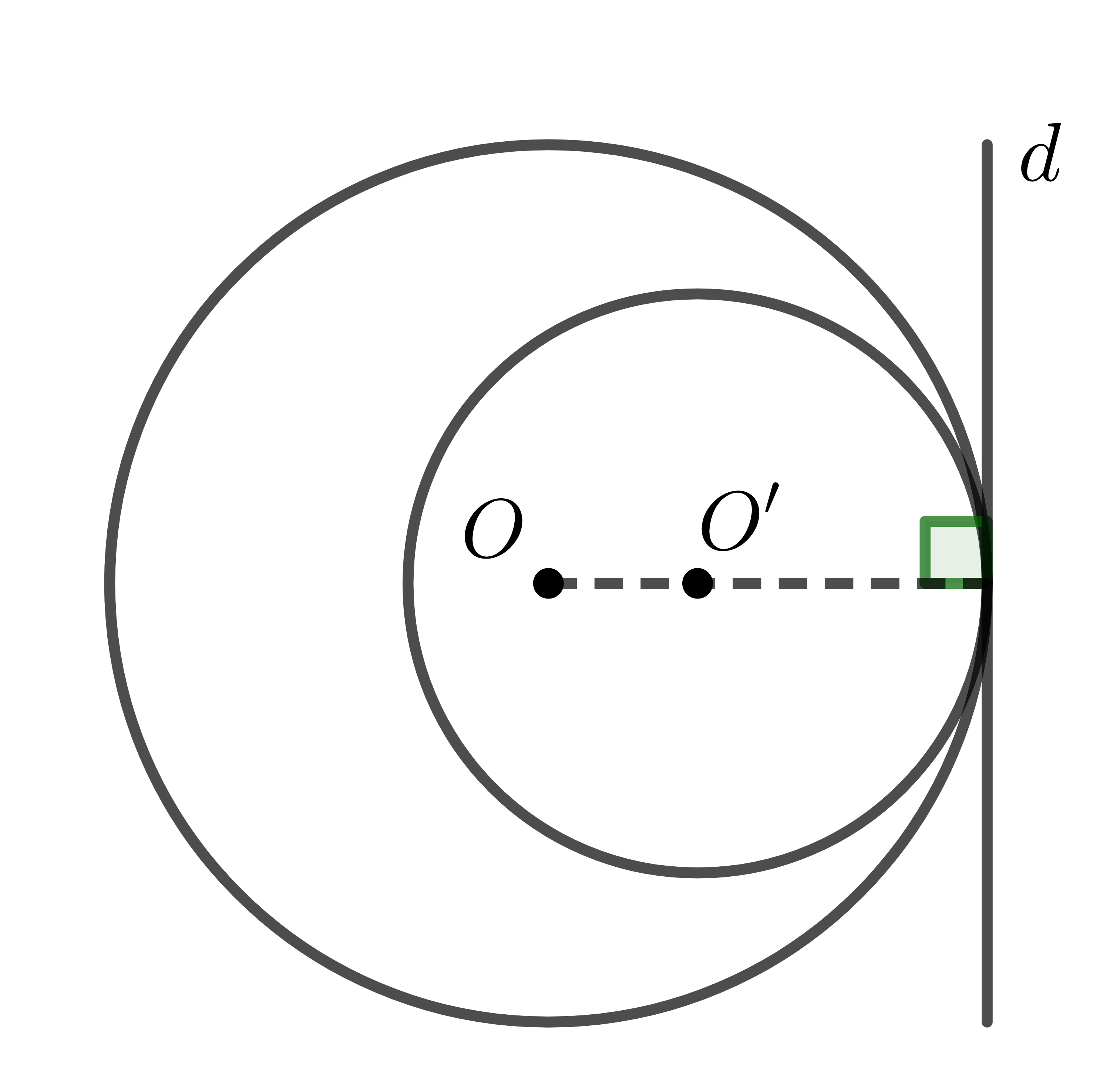
d) Hai đường tròn tiếp xúc trong
Hai đường tròn \(\left(O\right);\left(O'\right)\) tiếp xúc trong thì có đúng 1 tiếp tuyến chung là đường thẳng \(d\).
e) Hai đường tròn đựng nhau
Khi \(\left(O\right)\) đựng \(\left(O'\right)\) thì hai đường tròn này không có tiếp tuyến chung.

@423783@@57422@