I. Phân tích đa thức thành nhân tử

Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

Ví dụ 1: Trong các phép biến đổi sau đây, phép biến đổi nào là phân tích đa thức thành nhân tử?

a) x² - 9 = (x - 3)(x + 3);

b) 2x + 1 = x + 1 + x.

Hướng dẫn giải

a) Phép biến đổi x² - 9 = (x - 3)(x + 3) là phân tích đa thức thành nhân tử vì phép biến đổi đã viết đa thức  x² - 9 thành tích của hai đa thức.

b) Phép biến đổi 2x + 1 = x + 1 + x không phải là phân tích đa thức thành nhân tử vì phép biến đổi này chỉ viết đa thức 2x + 1 thành tổng hai đa thức khác.

II. Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử

1. Phân tích đa thức thành nhân tử bằng phương pháp vận dụng trực tiếp hằng đẳng thức

Ví dụ 2: Phân tích mỗi đa thức sau thành nhân tử:

a) x² - 4;        b) x³ - y³;          c) x³ + 8.

Hướng dẫn giải 

a) x² - 4 = (x - 2)(x + 2).

b) x³ - y³ = (x - y)(x² + xy + y²).

c) x³ + 8 = x³ + 2³ = (x + 2)(x² - 2x + 4).

Nhận xét: Cách làm như ví dụ trên được gọi là phân tích đa thức thành nhân tử bằng phương pháp vận dụng trực tiếp hằng đẳng thức.

2. Phân tích đa thức thành nhân tử bằng phương pháp vận dụng hằng đẳng thức thông qua nhóm số hạng và đặt nhân tử chung

Ví dụ 3: Phân tích các đa thức sau thành nhân tử:

a) \(x^2+2x+1-y^2\);              b) \(4x^2-9+3(2x -5)\).

Hướng dẫn giải

a) \(x^2+2x+1-y^2\)

\(=(x^2+2x+1)-y^2\\ =(x+1)^2-y^2\\ =(x+1-y)(x+1+y).\)

b) \(4x^2-9+3(2x -5)\)

\(=(4x^2-9)+3(2x-5) =(2x-5)(2x+5)+3(2x-5)\\ =(2x-5)(2x+5+3)\\ =(2x-5)(2x+8).\)

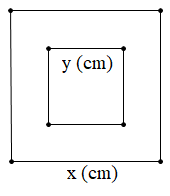
Ví dụ 4: Từ một miếng bìa có dạng hình vuông có cạnh x (cm). Bạn Hạnh khoét một hình vuông ở giữa có cạnh y (cm).

a) Viết công thức tính diện tích phần còn lại của miếng bìa dưới dạng tích.

b) Tính diện tích phần còn lại của miếng bìa biết cạnh của hình vuông ban đầu là 4 (cm), cạnh của hình vuông ở giữa là 2 (cm).

Hướng dẫn giải

Diện tích hình vuông ban đầu là \(x.x=x^2\) \((cm^2)\).

Diện tích hình vuông bị khoét đi là  \(y.y=y^2\) \((cm^2)\).

Diện tích phần còn lại của miếng bìa là 

\(x^2-y^2=(x-y)(x+y)\) \((cm^2)\).

b) Diện tích phần còn lại của miếng bìa là                    

\((4-2)(4+2)=12\) ​\((cm^2)\).​