Bài 3: Đồ thị của hàm số y = ax + b ( a khác 0)

1. Đồ thị hàm số \(y=ax+b\left(a\ne0\right)\)

Xét hàm số \(y=ax+b\) \(\left(a\ne0\right)\):

• Nếu \(b=0\): Ta có hàm số \(y=ax\). 

Ở lớp 7, ta đã biết: Đồ thị hàm số \(y=ax\) là một đường thẳng đi qua gốc tọa độ.

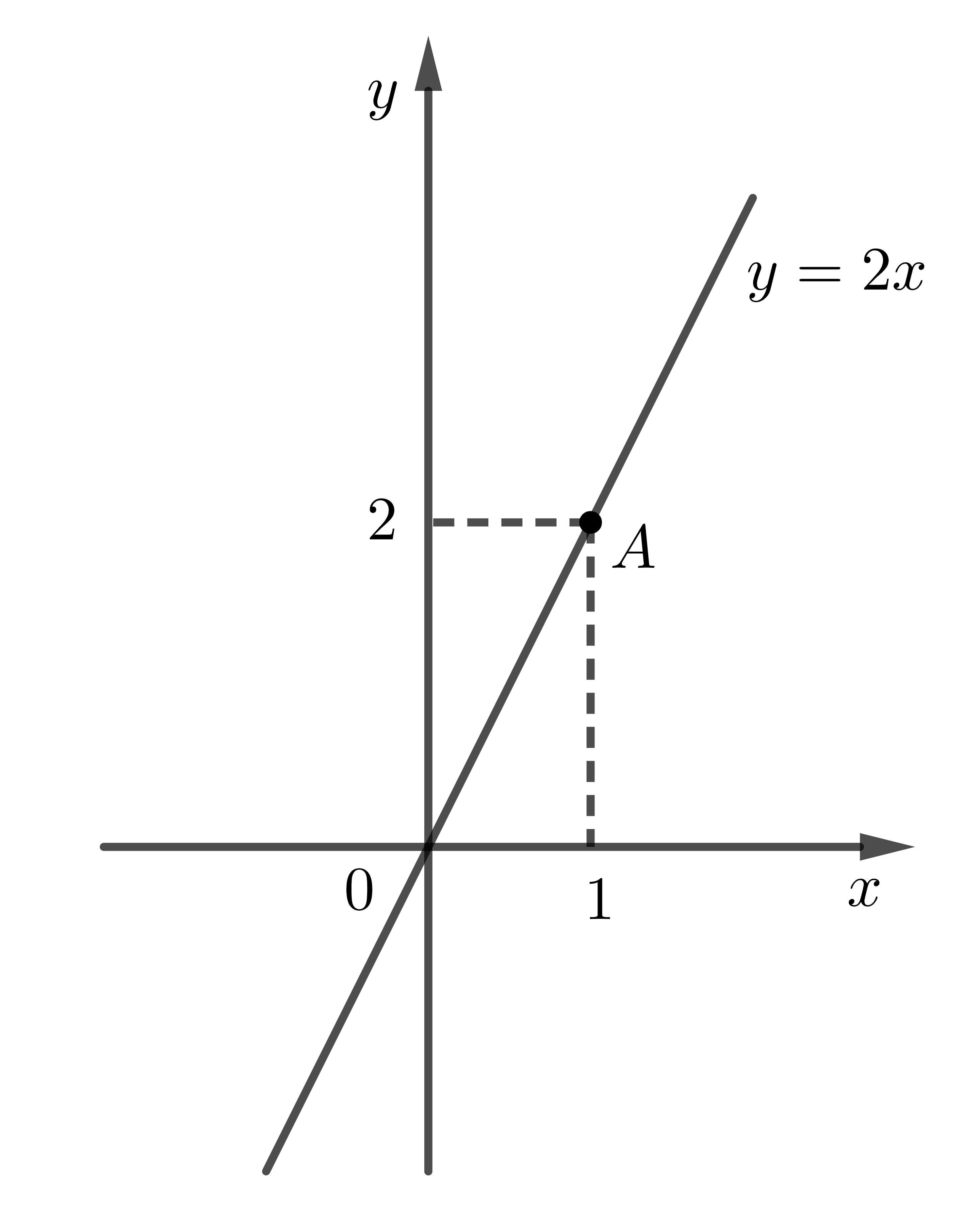
Ví dụ: Vẽ đồ thị hàm số \(y=2x\).

Cho \(x=1\Rightarrow y=2\) \(\Rightarrow A\left(1;2\right)\) là điểm thuộc đồ thị hàm số.

Nối \(O\) và \(A\), ta được đồ thị hàm số \(y=2x\) như sau:

• Nếu \(b\ne0\):

Ví dụ: Xét hàm số \(y=x+1\). Ta có bảng các giá trị của \(x\) và \(y\):

Nối các điểm có tọa độ \(\left(x,y\right)\) tương ứng như trên với nhau, ta thấy đồ thị hàm số cũng là một đường thẳng, và song song với đường thẳng \(y=x\).

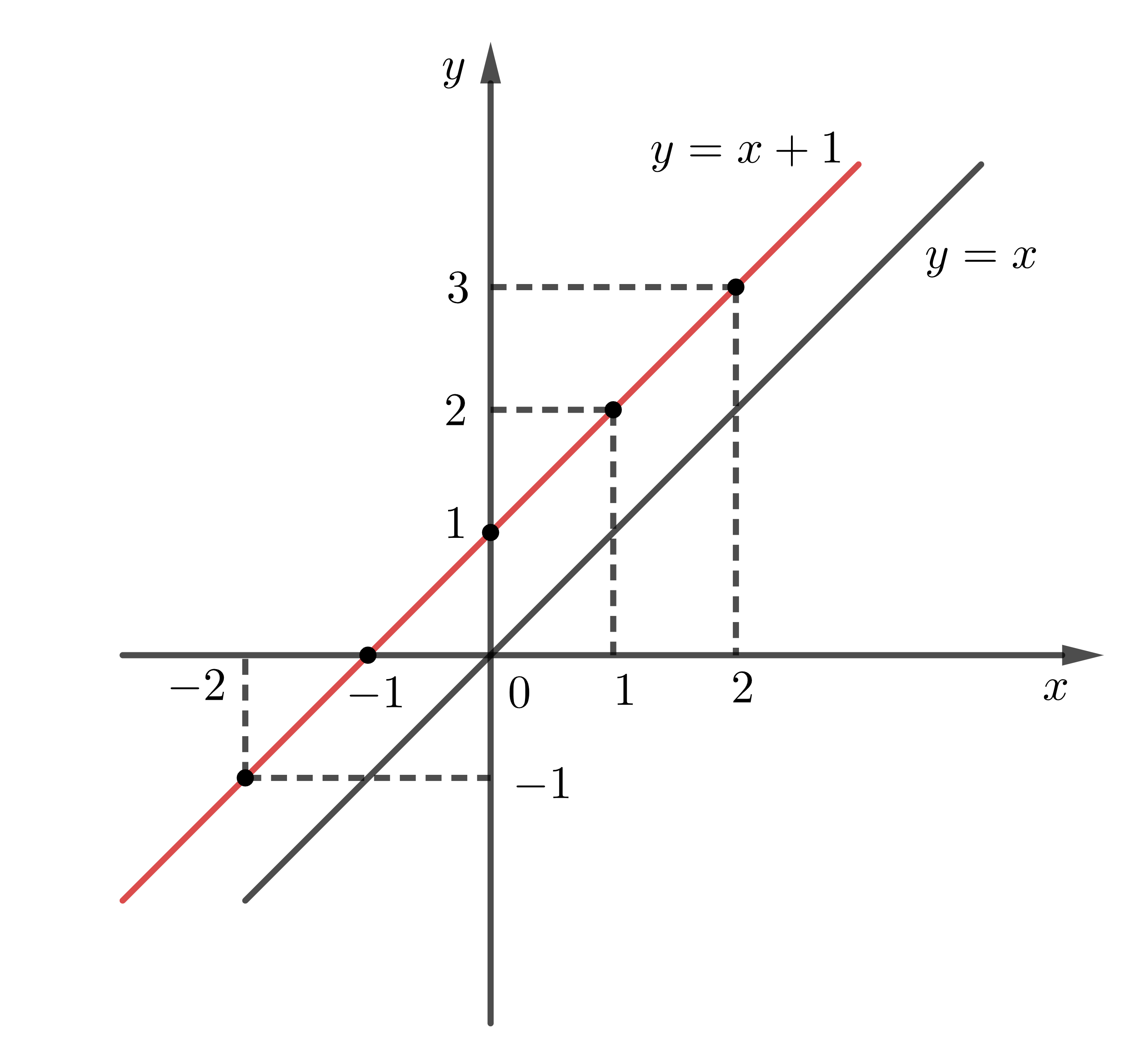
Như vậy, đồ thị hàm số \(y=ax+b\) cũng là một đường thẳng, song song với đồ thị hàm số \(y=ax\). Hơn nữa, ta dễ thấy: Khi \(x=0\) thì \(y=b\) \(\Rightarrow\) Đồ thị hàm số luôn đi qua điểm \(\left(0;b\right)\).

Tổng quát: 

Đồ thị hàm số \(y=ax+b\left(a\ne0\right)\) là một đường thẳng:

• Cắt trục tung tại điểm có tung độ bằng \(b\).

• Song song với đường thẳng \(y=ax\) nếu \(b\ne0\) và trùng với đường thẳng \(y=ax\) nếu \(b=0\).

Chú ý: Đồ thị hàm số \(y=ax+b\left(a\ne0\right)\) còn được gọi là đường thẳng \(y=ax+b\), còn \(b\) được gọi là tung độ gốc của đường thẳng.

2. Cách vẽ đồ thị hàm số \(y=ax+b\left(a\ne0\right)\)

• Khi \(b=0\) thì \(y=ax\). Đồ thị hàm số là đường thẳng đi qua gốc tọa độ \(O\left(0;0\right)\) và điểm \(A\left(1;a\right)\).

• Khi \(b\ne0\): 

Ta đã biết, đồ thị hàm số là một đường thẳng. Như vậy muốn vẽ đồ thị hàm số \(y=ax+b\), ta cần xác định hai điểm phân biệt thuộc đồ thị rồi vẽ đường thẳng nối hai điểm đó.

Thông thường trong thực hành, ta sẽ xác định hai điểm đặc biệt là giao điểm của đồ thị hàm số với hai trục tọa độ.

Bước 1: Với \(x=0\), ta có \(y=b\) \(\Rightarrow P\left(0;b\right)\) là giao điểm của đồ thị hàm số với trục tung.

Với \(y=0\), ta có \(x=-\dfrac{b}{a}\) \(Q\left(-\dfrac{b}{a};0\right)\) là giao điểm của đồ thị hàm số với trục hoành.

Bước 2: Vẽ đường thẳng đi qua hai điểm \(P,Q\), ta được đồ thị hàm số \(y=ax+b\).

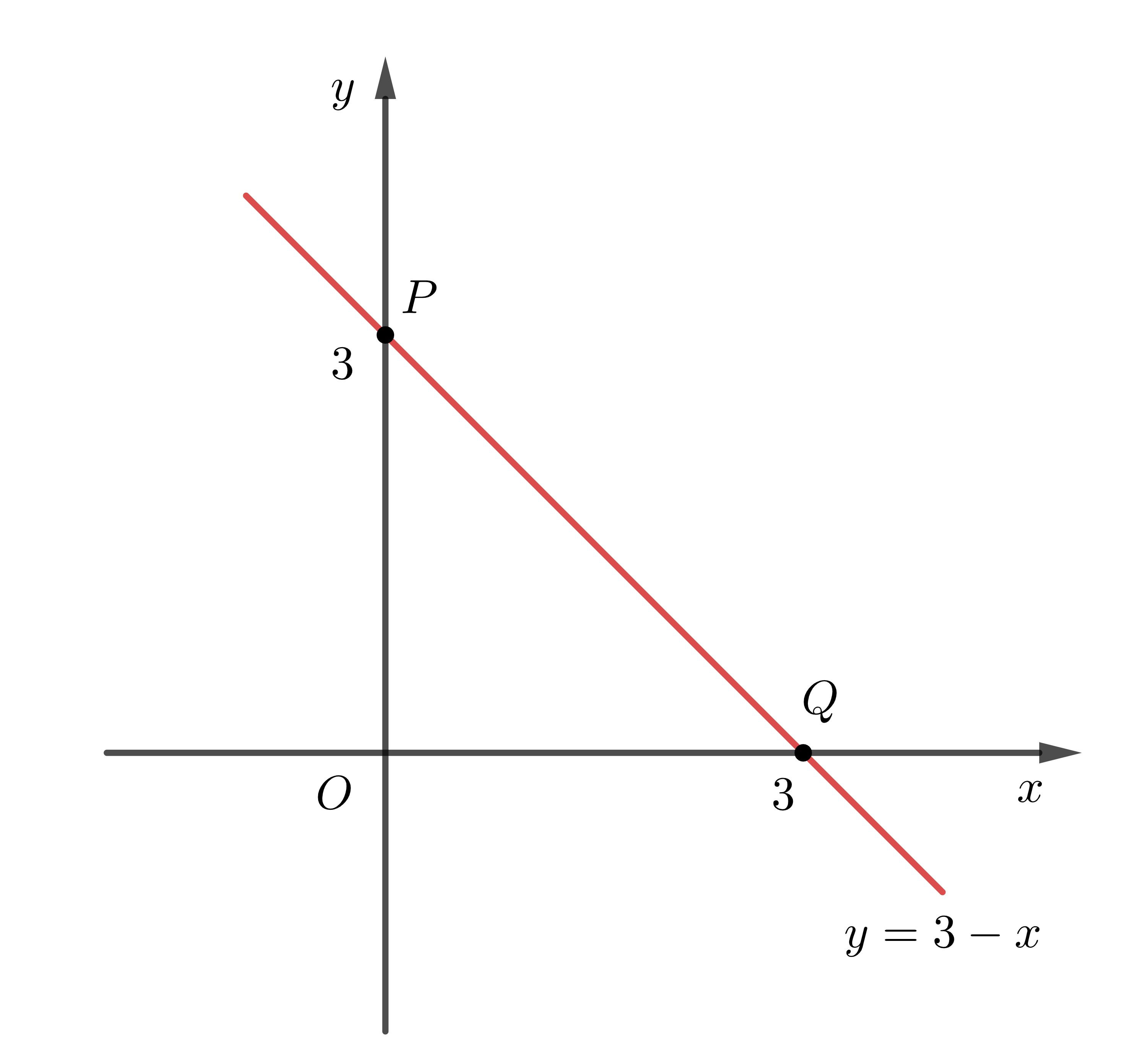
Ví dụ: Vẽ đồ thị hàm số \(y=3-x\).

Cho \(x=0\Rightarrow y=3\Rightarrow P\left(0;3\right)\) là giao điểm của đths với \(Oy\).

Cho \(y=0\Rightarrow x=3\Rightarrow Q\left(3;0\right)\) là giao điểm của đths với \(Ox\).

Nhận xét: Xét điểm \(A\left(x;y\right)\)

• Điểm đối xứng với \(A\) qua trục hoành \(Ox\) là điểm \(A_1\left(x;-y\right)\).
• Điểm đối xứng với \(A\) qua trục tung \(Oy\) là điểm \(A_2\left(-x;y\right)\).
• Điểm đối xứng với \(A\) qua gốc tọa độ \(O\) là d·\(A'\left(-x;-y\right)\).