Bài 1: Đa giác. Đa giác đều
Nội dung lý thuyết
Các phiên bản khác1. Khái niệm về đa giác
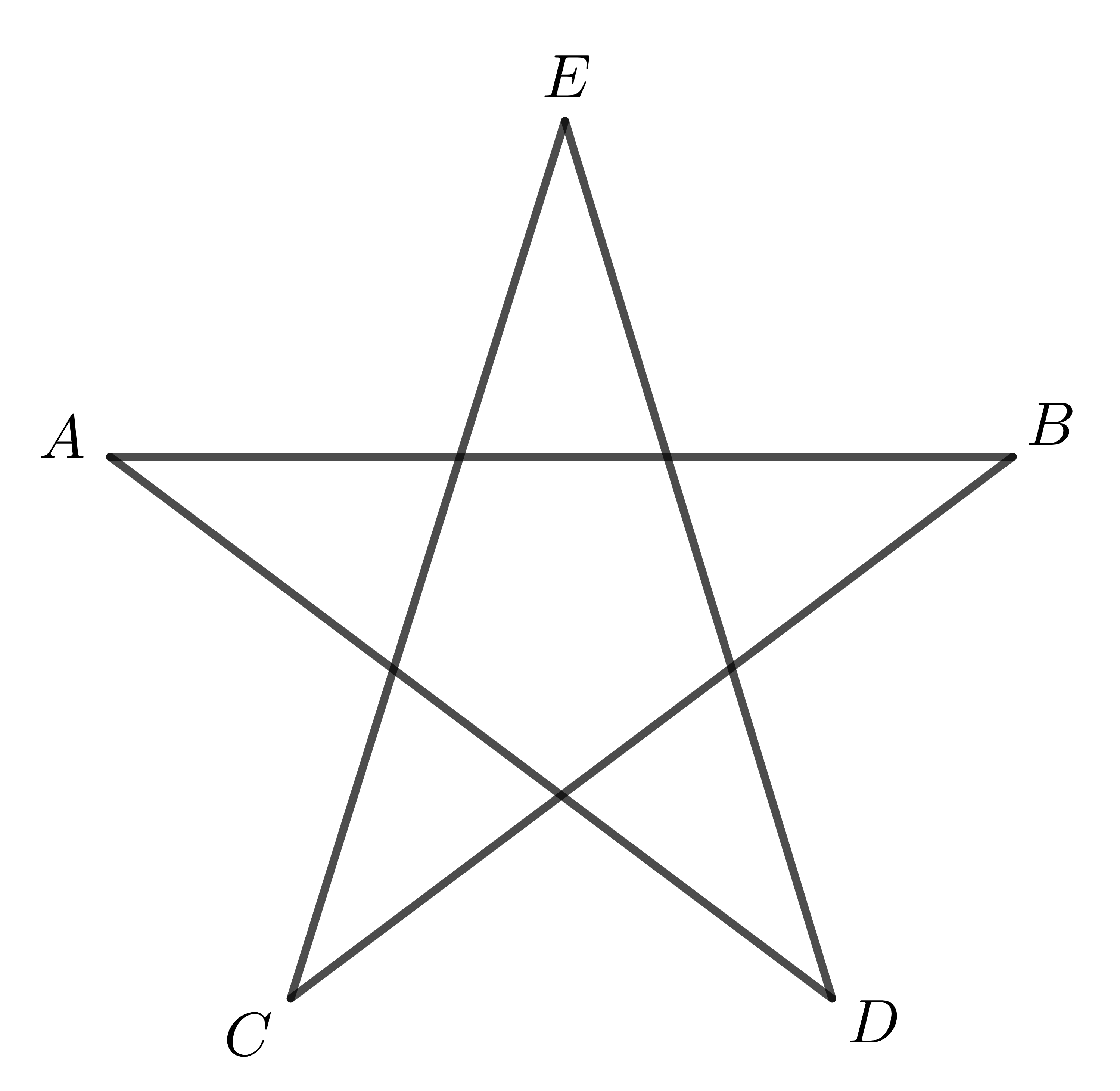
Cho các hình vẽ sau:
 |  |  |
 |  |  |
Mỗi hình trong các hình phía trên đều là một đa giác.
Trong hình 6, ta có định nghĩa:
Đa giác \(ABCDE\) là hình gồm có 5 đoạn thẳng \(AB,BC,CD,DE,AE\) trong đó bất kì đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng.
Các điểm \(A,B,C,D,E\) được gọi là các đỉnh của đa giác.
Các đoạn thẳng \(AB,BC,CD,DE,AE\) được gọi là các cạnh của đa giác đó.
Một cách tương tự, ta có thể định nghĩa được các đa giác còn lại trong hình.
Nhận xét: Mỗi đa giác đều có ít nhất là 3 cạnh. Tam giác, tứ giác cũng là các đa giác.
Trong các hình phía trên, hình 4, hình 5 và hình 6 được gọi là các đa giác lồi.
Định nghĩa: Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác.
Chú ý: Từ nay nếu không giải thích gì thêm, ta hiểu đa giác đang được nhắc đến là đa giác lồi.
Xét hình vẽ sau:
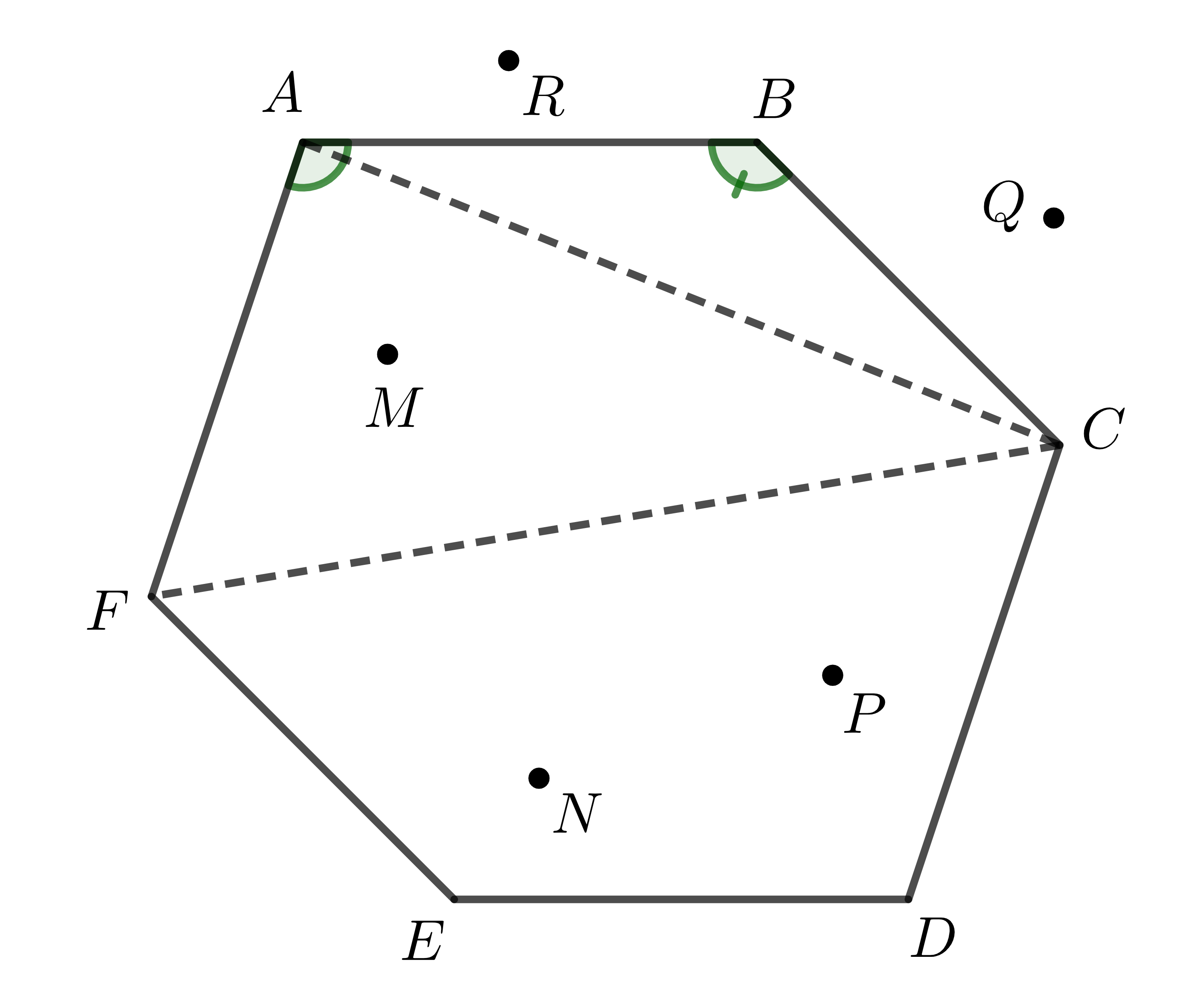
Hình trên biểu diễn đa giác \(ABCDEF\), trong đó:
- Các đỉnh là các điểm: \(A,B,C,D,E,F\). Trong đó các đỉnh kề nhau là: \(A\) và \(B\), \(B\) và \(C\), \(C\) và \(D\), ...
- Các cạnh là các đoạn thẳng: \(AB,BC,CD,DE,EF,AF\).
- Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau. Ví dụ: \(AC,CF\), ...
- Các góc: \(\widehat{A},\widehat{B},\widehat{C},\widehat{D},\widehat{E},\widehat{F}\).
- Các điểm nằm trong (điểm trong) của đa giác: \(M,N,P\).
- Các điểm nằm ngoài (điểm ngoài) của đa giác: \(Q,R\).
Lưu ý: Đa giác có \(n\) đỉnh (\(n\ge3\)) được gọi là hình \(n\) - giác hay hình \(n\) cạnh.
- Với \(n=3,4,5,6,8\), ta gọi là tam giác, tứ giác, ngũ giác, lục giác, bát giác.
- Với \(n=7,9,10\), ..., ta gọi là hình 7 cạnh, hình 9 cạnh, hình 10 cạnh, ...
Chú ý: Bằng các phép biến đổi sơ cấp, người ta chứng minh được các kết quả sau:
- Số đường chéo của một hình \(n\) - giác là: \(\dfrac{n\left(n-3\right)}{2}\).
- Tổng các góc trong một hình \(n\) - giác là: \(\left(n-2\right).180^0\).
Ví dụ: Số đường chéo của một hình ngũ giác là \(\dfrac{5\left(5-3\right)}{2}=5\), tổng các góc trong của nó là \(\left(5-2\right).180^0=540^0\).
@628572@
2. Đa giác đều
Định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau, tất cả các góc bằng nhau.

|  (hình vuông)
| 
|

| 
| 
|
Nhận xét: Từ định nghĩa, ta suy ra:
Số đo mỗi góc của hình \(n\) - giác đều là \(\dfrac{\left(n-2\right).180^0}{n}\).
Mỗi đa giác đều đều có số tâm đối xứng và trục đối xứng riêng.
Ví dụ:
+) Hình vuông có 1 tâm đối xứng là giao điểm 2 đường chéo, 4 trục đối xứng.
+) Hình ngũ giác đều không có tâm đối xứng, có 5 trục đối xứng.
Nhận xét:
+) Với \(n\) chẵn: Hình \(n\) - giác đều có 1 tâm đối xứng và \(n\) trục đối xứng (\(\dfrac{n}{2}\) đường thẳng nối các đỉnh đối nhau và \(\dfrac{n}{2}\) đường thẳng nối trung điểm hai cạnh đối nhau).
+) Với \(n\) lẻ: Hình \(n\) - giác đều có n trục đối xứng (\(n\) đường thẳng nối đỉnh và trung điểm cạnh đối của đỉnh đó) và không có tâm đối xứng.