§3. Các hệ thức lượng giác trong tam giác và giải tam giác
Nội dung lý thuyết
1. Định lí côsin
a) Bài toán: Trong tam giác \(ABC\) cho biết hai cạnh \(AB,AC\) và góc \(A\). Tính cạnh \(BC\).
Giải:
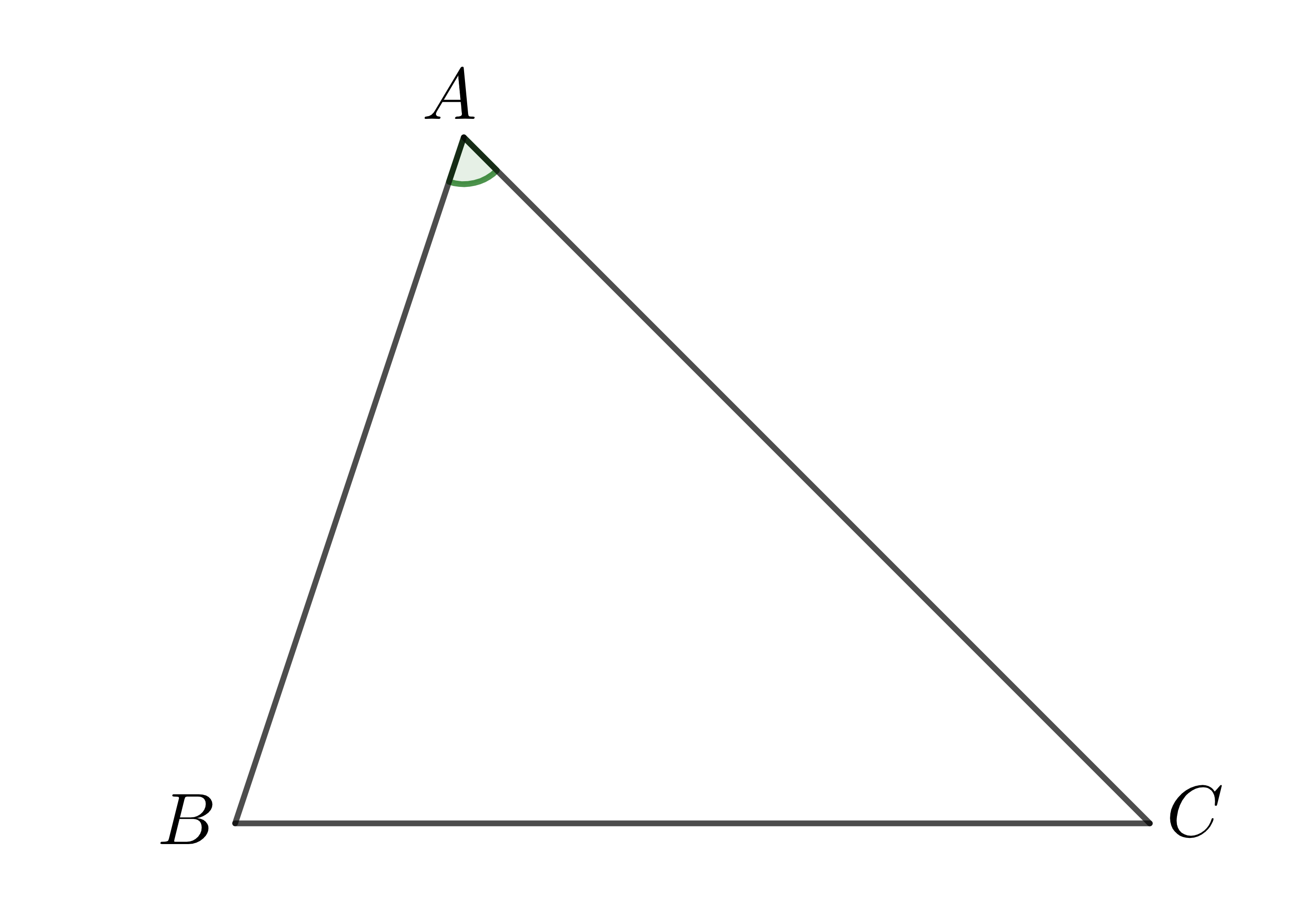
Ta có \(BC^2=\left|\overrightarrow{BC}\right|^2=\left(\overrightarrow{AC}-\overrightarrow{AB}\right)^2\)
\(=\overrightarrow{AC}^2+\overrightarrow{AB}^2-2\overrightarrow{AC}.\overrightarrow{AB}\)
\(BC^2=\overrightarrow{AC}^2+\overrightarrow{AB}^2-2\left|\overrightarrow{AC}\right|.\left|\overrightarrow{AB}\right|.\cos A\)
Vậy ta có \(BC^2=AC^2+AB^2-2AC.AB.\cos A\)
Nên \(BC=\sqrt{AC^2+AB^2-2AC.AB.\cos A}\)
Từ kết quả trên ta suy ra định lí:
b) Định lí côsin
Trong tam giác \(ABC\) bất kì với \(BC=a,CA=b,AB=c\) ta có:
\(a^2=b^2+c^2-2bc.\cos A\)
\(b^2=a^2+c^2-2ac.\cos B\)
\(c^2=a^2+b^2-2ab.\cos C\)
Ví dụ 1: Cho tam giác \(ABC\) có \(b=3cm,c=5cm\) và góc \(\widehat{A}=60^0\) . Tính số đo cạnh \(a\) của tam giác.
Giải:
Áp dụng định lí côsin trong tam giác \(ABC\) ta có:
\(a^2=b^2+c^2-2bc.\cos A=3^2+5^2-2.3.5.\cos60^0=9+25-30.\dfrac{1}{2}=19\)
\(\Rightarrow a=\sqrt{19}\)(cm)
Vậy độ dài cạnh \(a\) là \(\sqrt{19}\)cm.
Từ định lí côsin ta suy ra:
Hệ quả:
\(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\) ;
\(\cos B=\dfrac{a^2+c^2-b^2}{2ac}\) ;
\(\cos C=\dfrac{a^2+b^2-c^2}{2ab}\).
Ví dụ 2: Cho tam giác \(ABC\) có số đo các cạnh \(AB,BC,CA\) lần lượt là \(2cm,4cm,5cm\). Tính số đo góc \(A\).
Giải:
Áp dụng hệ quả trên ta có:
\(\cos A=\dfrac{AB^2+AC^2-BC^2}{2.AB.AC}=\dfrac{2^2+4^2-5^2}{2.2.4}=-\dfrac{5}{16}\)
Dùng máy tính bỏ túi ta tính được góc \(A\) là \(\approx108^0\).
@1963500@
c) Áp dụng: Tính độ dài đường trung tuyến của tam giác
Cho tam giác \(ABC\) có các cạnh \(BC=a,CA=b,AB=c\). Gọi \(m_a\), \(m_b\) và \(m_c\) là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh \(A,B,C\) của tam giác.
Ta có:
\(m_a^2=\dfrac{2\left(b^2+c^2\right)-a^2}{4}\) ;
\(m_b^2=\dfrac{2\left(a^2+c^2\right)-b^2}{4}\) ;
\(m_c^2=\dfrac{2\left(a^2+b^2\right)-c^2}{4}\).
Thật vậy, gọi \(M\) là trung điểm của cạnh \(BC\).

Áp dụng định lí côsin vào tam giác \(AMB\) ta có:
\(m_a^2=c^2+\left(\dfrac{a}{2}\right)^2-2c.\dfrac{a}{2}.\cos B=c^2+\dfrac{a^2}{4}-ac\cos B\)
Vì \(\cos B=\dfrac{a^2+c^2-b^2}{2ac}\) nên ta suy ra:
\(m_a^2=c^2+\dfrac{a^2}{4}-ac.\dfrac{a^2+c^2-b^2}{2ac}=\dfrac{2\left(b^2+c^2\right)-a^2}{4}\)
Chứng minh tương tự ta suy ra \(m_b^2=\dfrac{2\left(a^2+c^2\right)-b^2}{4}\) và \(m_c^2=\dfrac{2\left(a^2+b^2\right)-c^2}{4}\).
Ví dụ 3: Cho tam giác \(ABC\) có \(a=7cm,b=8cm,c=6cm\). Tính độ dài đường trung tuyến \(m_a\) của tam giác đó.
Giải:
Áp dụng công thức tính độ dài đường trung tuyến của tam giác ta có:
\(m_a^2=\dfrac{2\left(b^2+c^2\right)-a^2}{4}=\dfrac{2.\left(8^2+6^2\right)-7^2}{4}=\dfrac{151}{4}\)
\(\Rightarrow\) \(m_a=\sqrt{\dfrac{151}{4}}=\dfrac{\sqrt{151}}{2}\) (cm)
Vậy độ dài đường trung tuyến \(m_a\) là \(\dfrac{\sqrt{151}}{2}\)cm.
@1964135@
d) Ví dụ
Ví dụ 1: Cho tam giác \(ABC\) có các cạnh \(AC=10cm\), \(BC=16cm\) và góc \(\widehat{C}=110^0\). Tính độ dài cạnh \(AB\) và các góc \(A,B\) của tam giác.
Giải:

Đặt \(BC=a,CA=b,AB=c\).
Theo định lí côsin ta có:
\(c^2=a^2+b^2-2ab.\cos C=16^2+10^2-2.16.10.\cos110^0\)
\(c^2\approx465,44\)
Vậy \(c\approx\sqrt{465,44}\approx21,6\left(cm\right)\)
Theo hệ quả của định lí côsin ta có:
\(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\approx\dfrac{10^2+\left(21,6\right)^2-16^2}{2.10.\left(21,6\right)}\approx0,7188\)
Suy ra \(\widehat{A}\approx44^02'\), \(\widehat{B}=180^0-\left(\widehat{A}+\widehat{C}\right)\approx25^058'\)
2. Định lí sin
a) Định lí sin
Trong tam giác \(ABC\) bất kì với \(BC=a,CA=b,AB=c\) và \(R\) là bán kính đường tròn ngoại tiếp, ta có:
\(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\)
Ví dụ: Cho một tam giác đều cạnh \(a\). Tính bán kính đường tròn ngoại tiếp tam giác đều đó.
Giải:
Gọi bán kính ường tròn ngoại tiếp tam giác đều đó là \(R\)
Áp dụng định lí sin: \(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\)
Ta có: \(\dfrac{a}{\sin60^0}=2R\)
\(\Rightarrow R=\dfrac{a}{2\sin60^0}=\dfrac{a}{2.\dfrac{\sqrt{3}}{2}}=\dfrac{a}{\sqrt{3}}\)
b) Ví dụ: Cho tam giác \(ABC\) có \(\widehat{B}=20^0\), \(\widehat{C}=31^0\) và cạnh \(b=210cm\). Tính \(\widehat{A}\), các cạnh còn lại và bán kính \(R\) của đường tròn ngoại tiếp tam giác đó.
Giải:
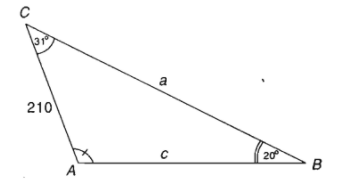
Ta có: \(\widehat{A}=180^0-\left(\widehat{B}+\widehat{C}\right)=180^0-\left(20^0+31^0\right)=129^0\)
Theo định lí sin ta có: \(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\)
Suy ra \(a=\dfrac{b\sin A}{\sin B}=\dfrac{210.\sin129^0}{\sin20^0}\approx477,2\) (cm)
\(c=\dfrac{b\sin C}{\sin B}=\dfrac{210.\sin31^0}{\sin20^0}\approx316,2\) (cm)
\(R=\dfrac{a}{2\sin A}=\dfrac{477,2}{2.\sin129^0}\approx307,02\) (cm)
@1965217@
3. Công thức tính diện tích tam giác
Ta kí hiệu \(h_a,h_b,h_c\) là các đường cao của tam giác \(ABC\) lần lượt kẻ từ các đỉnh \(A,B,C\) và \(S\) là diện tích của tam giác đó.
Ta đã biết \(S=\dfrac{1}{2}a.h_a\) với \(h_a=AH=AC.\sin C=b\sin C\) (kể cả \(\widehat{C}\) nhọn, tù hay vuông)
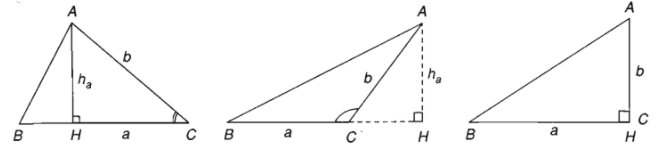
Do đó \(S=\dfrac{1}{2}ab\sin C\)
Tương tự ta cũng tính được \(S=\dfrac{1}{2}ac\sin B\) hay \(S=\dfrac{1}{2}bc\sin A\)
Từ đó ta có công thức \(S=\dfrac{1}{2}ab\sin C=\dfrac{1}{2}ac\sin B=\dfrac{1}{2}bc\sin A\).
Cho tam giác \(ABC\) bất kì với \(BC=a,CA=b,AB=c\) .
Gọi \(R,r\) lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp tam giác và \(p=\dfrac{a+b+c}{2}\) là nửa chu vi của tam giác.
Diện tích \(S\) của tam giác \(ABC\) được tính theo một trong các công thức:
\(S=\dfrac{1}{2}ab\sin C=\dfrac{1}{2}ac\sin B=\dfrac{1}{2}bc\sin A\) (1)
\(S=\dfrac{abc}{4R}\) (2)
\(S=pr\) (3)
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) (công thức Hê-rông) (4)
Ví dụ 1: Tam giác \(ABC\) có các cạnh \(a=13m\), \(b=14m\) và \(c=15m\).
a) Tính diện tích tam giác \(ABC\) ;
b) Tính bán kính đường tròn nội tiếp và ngoại tiếp tam giác \(ABC\).
Giải:
a) Ta có \(p=\dfrac{a+b+c}{2}=\dfrac{13+14+15}{2}=21\)
Áp dụng công thức Hê-rông ta có:
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{21.\left(21-13\right)\left(21-14\right)\left(21-15\right)}=84\) (m2)
b) Áp dụng công thức \(S=pr\) ta suy ra \(r=\dfrac{S}{p}=\dfrac{84}{21}=4\) (m)
Vậy bán kính đường tròn nội tiếp tam giác \(ABC\) là \(4m\).
Từ công thức \(S=\dfrac{abc}{4R}\) ta suy ra \(R=\dfrac{abc}{4S}=\dfrac{13.14.15}{4.84}=8,125\) (m)
Vậy bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(8,125m\).
Ví dụ 2: Tam giác \(ABC\) có cạnh \(a=2\sqrt{3}\), cạnh \(b=2\) và góc \(\widehat{C}=30^0\). Tính cạnh \(c\), góc \(\widehat{A}\) và diện tích tam giác đó.
Giải:
Theo định lí côsin ta có:
\(c^2=a^2+b^2-2ab\cos C=\left(2\sqrt{3}\right)^2+2^2-2.2\sqrt{3}.2.\cos30^0=4\)
\(\Rightarrow c=\sqrt{4}=2\)
Vậy cạnh \(c=2\)
Ta thấy tam giác \(ABC\) có \(b=c=2\) hay \(AC=AB=2\) suy ra tam giác \(ABC\) cân tại \(A\)
\(\Rightarrow\widehat{B}=\widehat{C}=30^0\)
Do đó \(\widehat{A}=180^0-30^0-30^0=120^0\)
Vậy góc \(\widehat{A}=120^0\)
Ta có \(S=\dfrac{1}{2}ac\sin B=\dfrac{1}{2}.2\sqrt{3}.2.\sin30^0=\sqrt{3}\)
Vậy diện tích tam giác \(ABC\) là \(\sqrt{3}\) (đơn vị diện tích)
@1965057@
4. Giải tam giác và ứng dụng vào việc đo đạc
a) Giải tam giác
Giải tam giác là tìm một số yếu tố của tam giác khi cho biết các yếu tố khác.
Ví dụ 1: Cho tam giác \(ABC\) biết cạnh \(a=17,4m\) , \(\widehat{B}=44^030'\) và \(\widehat{C}=64^0\). Tính góc \(\widehat{A}\) và các cạnh \(b,c\).
Giải:
Ta có: \(\widehat{A}=180^0-\left(\widehat{B}+\widehat{C}\right)=180^0-\left(44^030'+64^0\right)=71^030'\)
Theo định lí sin ta có \(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
do đó \(b=\dfrac{a\sin B}{\sin A}=\dfrac{17,4.\sin44^030'}{\sin71^030'}\approx12,9\left(m\right)\)
\(c=\dfrac{a\sin C}{\sin A}=\dfrac{17,4.\sin64^0}{\sin71^030'}\approx16,5\left(m\right)\)
Ví dụ 2: Cho tam giác \(ABC\) có cạnh \(a=49,4cm\), \(b=26,4cm\) và \(\widehat{C}=47^020'\). Tính cạnh \(c\), góc \(\widehat{A}\) và góc \(\widehat{B}\).
Giải:
Theo định lí côsin ta có \(c^2=a^2+b^2-2ab\cos C\)
Nên \(c^2=\left(49,4\right)^2+\left(26,4\right)^2-2.49,4.26,4.\cos47^020'\approx1369,66\)
Suy ra \(c\approx\sqrt{1369,66}\approx37\left(cm\right)\)
Ta có \(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\approx\dfrac{\left(26,4\right)^2+37^2-\left(49,4\right)^2}{2.26,4.37}\approx-0,191\)
Như vậy góc \(\widehat{A}\) tù và ta có \(\widehat{A}\approx101^0\).
Do đó \(\widehat{B}=180^0-\left(\widehat{A}+\widehat{C}\right)\approx31^040'\)
Ví dụ 3: Cho tam giác \(ABC\) có cạnh \(a=24cm\), \(b=13cm\) và \(c=15cm\). Tính diện tích \(S\) của tam giác và bán kính \(r\) của đường tròn nội tiếp tam giác.
Giải:
Theo định lí côsin ta có \(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\approx\dfrac{13^2+15^2-24^2}{2.13.15}\approx-0,4667\)
Như vậy góc \(\widehat{A}\) tù và ta tính được \(\widehat{A}\approx117^049'\) \(\Rightarrow\sin A\approx0,88\)
Ta có \(S=\dfrac{1}{2}bc\sin A\approx\dfrac{1}{2}13.15.0,88=85,8\left(cm^2\right)\)
Áp dụng công thức \(S=pr\) ta có \(r=\dfrac{S}{p}\).
Vì \(p=\dfrac{24+13+15}{2}=26\left(cm\right)\) nên \(r\approx\dfrac{85,8}{26}=3,3\left(cm\right)\)
b) Ứng dụng vào việc đo đạc
Bài toán 1: Đo chiều cao của một cái tháp mà không thể đến được chân tháp.
Giả sử \(CD=h\) là chiều cao của tháp trong đó \(C\) là chân tháp. Chọn hai điểm \(A,B\) trên mặt đất sao cho ba điểm \(A,B,C\) thẳng hàng. Ta đo khoảng cách \(AB\) và các góc \(\widehat{CAD},\widehat{CBD}\). Chẳng hạn đo được \(AB=24m,\widehat{CAD}=\alpha=63^0,\widehat{CBD}=\beta=48^0\).
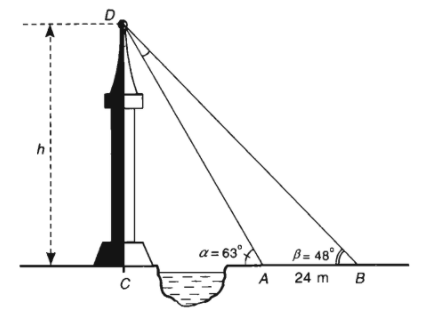
Khi đó chiều cao \(h\) của tháp được tính như sau:
Áp dụng định lí sin vào tam giác \(ABD\) có: \(\dfrac{AD}{\sin\beta}=\dfrac{AB}{\sin D}\)
Ta có \(\alpha=\widehat{D}+\beta\) nên \(\widehat{D}=63^0-48^0=15^0\)
Do đó \(AD=\dfrac{AB.\sin\beta}{\sin D}=\dfrac{24.\sin48^0}{\sin15^0}\approx68,91\)
Trong tam giác vuông \(ACD\) có \(h=CD=AD\sin\alpha\approx61,4\left(m\right)\)
Bài toán 2: Tính khoảng cách từ một địa điểm trẻn bờ sông đến một gốc cây trên một cù lao ở giữa sông.
Để đo khoảng cách từ một điểm \(A\) trên bờ sông đến gốc cây \(C\) trên cù lao giữa sông, người ta chọn một điểm \(B\) cùng ở trên bờ với \(A\) sao cho từ \(A\) và \(B\) có thể nhìn thấy điểm \(C\). Ta đo khoảng cách \(AB\), góc \(\widehat{CAB},\widehat{CBA}\). Chẳng hạn đo được \(AB=40m\), \(\widehat{CAB}=\alpha=45^0,\widehat{CBA}=\beta=70^0\).
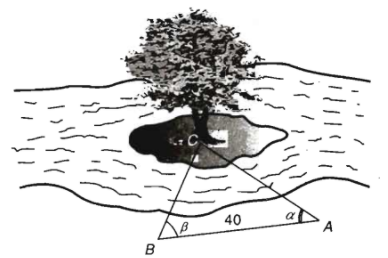
Khi đó khoảng cách \(AC\) được tính như sau:
Áp dụng định lí sin vào tam giác \(ABC\) ta có: \(\dfrac{AC}{\sin B}=\dfrac{AB}{\sin C}\)
Vì \(\sin C=\sin\left(\alpha+\beta\right)\) nên \(AC=\dfrac{AB.\sin\beta}{\sin\left(\alpha+\beta\right)}=\dfrac{40.\sin70^0}{\sin115^0}\approx41,47\left(m\right)\)
Vậy \(AC\approx41,47\left(m\right)\).